将一副直角三角板按如图1摆放在直线AD上（直角三角板OBC和直角三角板MON，∠OBC=90°，∠BOC=45°，∠MON=90°，∠MNO=30°），保持三角板OBC不动，将三角板MON绕点O以每秒2°的速度顺时针方向旋转t秒．

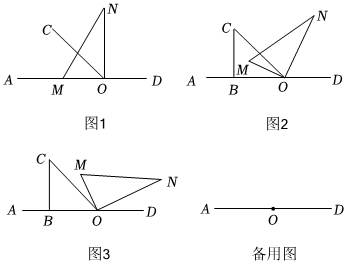
（1）如图2，当t=

11.25

11.25

秒时，OM平分∠AOC．
（2）继续旋转三角板MON，如图3，使得OM、ON同时在直线OC的右侧，猜想∠NOC与∠AOM有怎样的数量关系？并说明理由．
（3）直线AD的位置不变，若在三角板MON开始顺时针旋转的同时，另一个三角板OBC也绕点O以每秒6°的速度顺时针旋转，当ON旋转至射线OD上时，两个三角板同时停止运动，当t多少秒时，∠BON=60°．