完成下列分析过程．
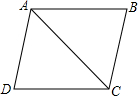
如图所示，已知AB∥DC，AD∥BC，求证：AB=CD．
分析：要证AB=CD，只要证△ABCABC≌△CDACDA；需先证∠BACBAC=∠DCADCA，∠ACBACB=∠CADCAD．由已知“ABAB∥DCDC”，可推出∠BACBAC=∠DCADCA，ADAD∥BCBC，可推出∠ACBACB=∠CADCAD，且公共边ACAC=CACA，因此，可以根据“角边角公理（ASA）角边角公理（ASA）”判定△ABCABC≌△CDACDA．
【考点】全等三角形的判定．
【答案】ABC；CDA；BAC；DCA；ACB；CAD；AB；DC；BAC；DCA；AD；BC；ACB；CAD；AC；CA；角边角公理（ASA）；ABC；CDA
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：51引用：2难度：0.7
相似题
-
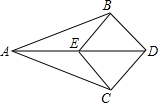1．如图，已知AD平分∠BAC，且∠ABD=∠ACD，则由“AAS“可直接判定△≌△．发布：2025/6/22 23:30:1组卷：104引用：4难度：0.7 -
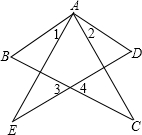2．如图，要用“SAS”证△ABC≌△ADE，若已知AB=AD，AC=AE，则还需条件（ ）发布：2025/6/23 0:30:1组卷：580引用：16难度：0.9 -
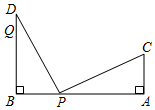
3．如图，AB=12米，CA⊥AB于点A，且AC=4米，DB⊥AB于点B，点P从B向A运动，每分钟走1米，点Q从点B沿BD方向运动，每分钟走2米，现在P、Q两点同时出发，那么运动 分钟后，△CPA≌△PQB．
发布：2025/6/22 23:0:1组卷：94引用：1难度：0.5
