小明在学习中遇到这样一个问题:
如图1,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于D.猜想∠B、∠C、∠EAD的数量关系.
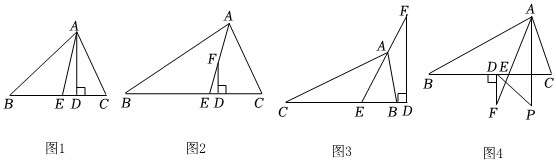
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入∠B、∠C的值求∠EAD值,得到下面几组对应值:
| ∠B/度 | 10 | 20 | 30 | 20 | 20 |
| ∠C/度 | 70 | 70 | 60 | 60 | 80 |
| ∠EAD/度 | 30 | a | 15 | 20 | 30 |
25
25
,于是得到∠B、∠C、∠EAD的数量关系为 ∠
EAD
=
1
2
(
∠
C
-
∠
B
)
∠
EAD
=
1
2
(
∠
C
-
∠
B
)
【变式应用】
(2)小明继续探究,在图2中,∠B=35°,∠C=75°,其他条件不变,若把“AD⊥BC于点D”改为“F是线段AE上一点,FD⊥BC于点D”.求∠DFE的度数,并写出∠DFE与∠B、∠C的数量关系.
【思维发散】
(3)小明突发奇想,交换B、C两个字母位置,在图3中,若把(2)中的“点P在线段AE上”改为“点F是EA延长线上一点”其余条件不变,当∠ABC=80°,∠C=24°时,∠F度数为
28
28
°.【能力提升】
(4)在图4中,若点F在AE的延长线上,FD⊥BC于点D,∠B=x,∠C=y,其余条件不变,分别作出∠CAE和∠EDF的角平分线,交于点P,试用x,y表示∠P=
1
4
(
3
y
-
x
)
1
4
(
3
y
-
x
)
【答案】25;;28;
∠
EAD
=
1
2
(
∠
C
-
∠
B
)
1
4
(
3
y
-
x
)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/6 2:0:8组卷:118引用:2难度:0.4
相似题
-
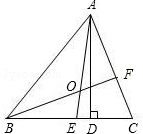 1.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.发布:2025/6/13 5:30:2组卷:1048引用:12难度:0.5
1.如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.发布:2025/6/13 5:30:2组卷:1048引用:12难度:0.5 -
2.若一个三角形三个内角度数的比为2:3:4,那么这个三角形是( )
发布:2025/6/13 6:0:2组卷:799引用:64难度:0.9 -
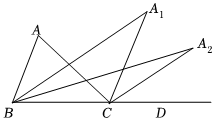 3.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,…;依此规律得∠A2022,则∠A2022=.发布:2025/6/13 5:0:1组卷:124引用:1难度:0.6
3.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,…;依此规律得∠A2022,则∠A2022=.发布:2025/6/13 5:0:1组卷:124引用:1难度:0.6


