材料阅读:
在学习绝对值时,我们知道了绝对值的几何含义,如|3-1]表示3、1在数轴上对应的两点之间的距离;|3+1|=|3-(-1)|所以|3+1|表示3、-1在数轴上对应的两点之间的距离;|3|=|3-0|,所以|3|表示3在数轴上对应的点到原点的距离.综上,数轴上A、B两点对应的数分别为a、b,且A、B两点之间的距离可以表示为AB,则AB=|a-b|(或|b-a|).
(1)数轴上表示x、-2在数轴上对应的两点之间的距离为 x+2
x+2
;
(2)表示x、5在数轴上对应的两点之间的距离与表示x、-1在数轴上对应的两点之间的距离之和为 x+1
+x-5
x+1
+x-5
,当x满足 -1≤x≤5-1≤x≤5时,该式子取得最小值,最小值为 66;
(3)当x满足 -3≤x≤3-3≤x≤3时,式子|x-3|+|2x+6|+|x-4|取得最小值,最小值为 1313;
(4)若(|x-1|+|x-3|+|x-7|)×(y+2|+|y-1|+|y-3|+|y-5|)=54,直接写出x+y的最大值 66和x-y的最大值 22.
x + 2 |
x + 2 |
x + 1 |
x - 5 |
x + 1 |
x - 5 |
【答案】
;
+
;-1≤x≤5;6;-3≤x≤3;13;6;2
x + 2 |
x + 1 |
x - 5 |
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/12 19:0:8组卷:355引用:1难度:0.3
相似题
-
 1.已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )发布:2025/7/1 13:0:6组卷:225引用:29难度:0.9
1.已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )发布:2025/7/1 13:0:6组卷:225引用:29难度:0.9 -
2.以下几句话:①数轴上的点表示的数都是有理数;②没有最大的负有理数;③正整数和负整数统称为整数;④不是负数的整数是正整数;⑤非正整数就是指负整数、0、正分数和负分数.其中正确的有( )
发布:2025/6/25 8:30:1组卷:273引用:2难度:0.8 -
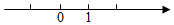 3.在纸面上有一数轴(如图),现折叠纸面.
3.在纸面上有一数轴(如图),现折叠纸面.
(1)若1表示的点与-1表示的点重合,则-2表示的点与表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
①6表示的点与表示的点重合;
②若数轴上A,B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,则点A表示的数是,点B表示的数是;
(3)现把一根无拉伸状态的橡皮筋AB的一端A固定在原点,另一端B恰好能与数轴上表示1的点重合.作如下操作:把橡皮筋对折,使橡皮筋的B端与A端重合后,再均匀的拉伸至与数轴上表示1的点重合的位置,这一过程称为一次操作;问:在第三次操作后,恰好被拉到与1重合的所有的点所对应的数之和是.发布:2025/6/25 8:30:1组卷:82引用:1难度:0.7


