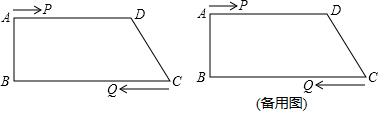
如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm,AD=20cm,BC=24cm,P、Q分别从A、C同时出发，向D，B运动．当一个点到达端点时，停止运动，另一个点也停止运动．
（1）如果P、Q的速度分别为1cm/s和3cm/s.运动时间为t秒，则t为何值时，PQ=DC．并说明理由．
（2）如果P的速度为1cm/s,其他条件不变，要使四边形APQB是矩形，且矩形的长宽之比为2：1，求Q点运动的速度．
【考点】矩形的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/15 8:0:8组卷：2480引用：6难度：0.1
相似题
-
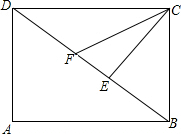1．如图，已知平行四边形ABCD中，∠BCD=90°，CE⊥BD于E，CF平分∠DCE与DB交于点F，
（1）求证：BF=BC；
（2）若AB=4cm,AD=3cm,求CF．发布：2025/6/17 19:0:1组卷：998引用：2难度：0.5 -
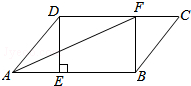2．在▱ABCD中，过点D作DE⊥AB于点E，点F在CD上，AE=CF，连接BF、AF．
（1）求证：四边形DEBF是矩形；
（2）若AF平分∠DAB，AE=3，DE=4．则AF长为．发布：2025/6/16 7:0:1组卷：791引用：7难度：0.5 -
3．如图，在菱形ABCD中，AC、BD交于点O，AC=6，BD=8，若DE∥AC，CE∥BD，则OE的长为．发布：2025/6/17 2:0:1组卷：1492引用：8难度：0.7
