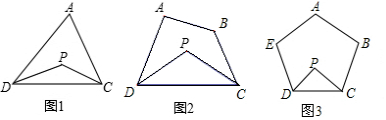
（1）已知：如图1，P为△ADC内一点，DP、CP分别平分∠ADC和∠ACD．如果∠A=50°，那么∠P=

115

115

°；如果∠A=100°，那么∠P=

140°

140°

．（直接写出答案，不必说明理由）
（2）如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，请直接写出∠P与∠A+∠B的数量关系：

∠P=

1

2

（∠A+∠B）

∠P=

1

2

（∠A+∠B）

（直接写出答案，不必说明理由）
（3）如图3，P为五边形ABCDE内一点；DP、CP分别平分∠EDC、∠BCD，“试探究∠P与∠A+∠B+∠E的数量关系，并说明理由．