某商店如果将进货价为8元的商品按每件10元售出，每天可销售200件，现在采用提高售价，减少进货量的方法增加利润，已知这种商品每涨价1元，其销量就减少20件．使每天获得利润700元，请你帮忙确定售价．
解：用含x的代数式填空
设这种商品涨价x元，则每件盈利 （10+x-8）（10+x-8）元，每天可售出 200-20×x1200-20×x1件，销售这些商品可盈利 （10+x-8）（200-20×x1）（10+x-8）（200-20×x1）元，当盈利700元时，可列方程 （10+x-8）（200-20×x1）=700（10+x-8）（200-20×x1）=700，解方程得 x=3或x=5x=3或x=5．
此时，商品售价为 13元或15元13元或15元元
答：把售价定为每件13元或15元能使每天利润达到700元把售价定为每件13元或15元能使每天利润达到700元．
200
-
20
×
x
1
200
-
20
×
x
1
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
=
700
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
=
700
【考点】一元二次方程的应用．
【答案】（10+x-8）；；；；x=3或x=5；13元或15元；把售价定为每件13元或15元能使每天利润达到700元
200
-
20
×
x
1
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
（
10
+
x
-
8
）
（
200
-
20
×
x
1
）
=
700
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/6 17:0:2组卷：111引用：3难度：0.5
相似题
-
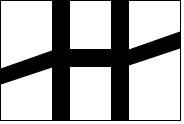1．某单位准备将院内一块长30米，宽20米的长方形空地建成一个矩形花园，要求在花园中修两条纵向平行和一条横向弯折的小道，剩余地方种植花草．如图所示，要使种植花草的面积为532平方米，那么小道进出口的宽度应为 米．（注：所有小道进出口的宽度相等，且每段小道均为平行四边形）发布：2025/6/16 11:0:1组卷：243引用：4难度：0.8 -
2．某公园准备围建一个矩形花园ABCD，其中一边靠墙，其他三边用长为54米的篱笆围成，已知墙EF长为28米，并且与墙平行的一面BC上要预留2米宽的入口（如图MN所示，不用围篱笆），若花园的面积为320平方米，则AB=．发布：2025/6/16 8:0:2组卷：831引用：4难度：0.6 -
3．小张2019年末开了一家商店，受疫情影响，2020年4月份才开始盈利，4月份盈利6000元，6月份盈利达到7260元，且从4月份到6月份，每月盈利的平均增长率都相同．
（1）求每月盈利的平均增长率．
（2）按照这个平均增长率，预计2020年7月份这家商店的盈利将达到多少元？发布：2025/6/16 10:30:1组卷：2813引用：27难度：0.8
