从三角形（不是等腰三角形）一个顶点引出的一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形有两角对应相等，我们把这条线段叫做这个三角形的“优美分割线”．
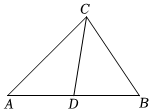
（1）如图，在△ABC中，CD为角平分线．∠A=40°，∠B=60°，求证：CD为△ABC的“优美分割线”；
（2）在△ABC中，∠A=46°，CD为△ABC的“优美分割线”且△ACD为等腰三角形，求∠ACB的度数；
（3）在△ABC中．∠A=30°，AC=6，CD为△ABC的“优美分割线”，且△ACD是等腰三角形，求线段BD的长．
【答案】（1）证明见解答过程；
（2）∠ACB的度数是92°或113°；
（3）3-3或．
（2）∠ACB的度数是92°或113°；
（3）3
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/6 8:0:9组卷：166引用：1难度：0.5
