阅读材料,回答下列问题:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示.
在数轴上,有理数3与1对应的两点之间的距离为|3-1|=2;
在数轴上,有理数5与-2对应的两点之间的距离为|5-(-2)|=7;
在数轴上,有理数-2与3对应的两点之间的距离为|-2-3|=5;
在数轴上,有理数-8与-5对应的两点之间的距离为|-8-(-5)|=3;
……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a-b|或|b-a|,记为|AB|=|a-b|=|b-a|.
(1)数轴上有理数-10与-5对应的两点之间的距离等于 55;
(2)数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为 |x+5||x+5|;
(3)若数轴上有理数x与-1对应的两点A,B之间的距离|AB|=2,则x等于 1或-31或-3;
(4)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为-2,动点P表示的数为x.若点P在点M,N之间,则|x+2|+|x-4|=66;若|x+2|+|x-4|=10,则x=x=6或-4x=6或-4.

【答案】5;|x+5|;1或-3;6;x=6或-4
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/28 6:0:4组卷:133引用:1难度:0.5
相似题
-
1.已知2x+4=m,用含m的代数式表示2x正确的是( )
发布:2025/5/24 2:0:8组卷:249引用:4难度:0.7 -
 2.方孔铜钱应天圆地方之说,古代入们认为天是圆的(圆形),地是方的(正方形),所以秦朝以后铸钱大多以“外圆内方”为型.如图中是一枚清代的“乾隆通宝”,“外圆”直径为a,内方边长为b,则这枚钱币的面积可以表示为( )发布:2025/5/24 13:30:2组卷:138引用:7难度:0.7
2.方孔铜钱应天圆地方之说,古代入们认为天是圆的(圆形),地是方的(正方形),所以秦朝以后铸钱大多以“外圆内方”为型.如图中是一枚清代的“乾隆通宝”,“外圆”直径为a,内方边长为b,则这枚钱币的面积可以表示为( )发布:2025/5/24 13:30:2组卷:138引用:7难度:0.7 -
3.如图,数轴上点O为原点,点A,B,C表示的数分别是m+1,2-m,9-4m.
(1)AB=(用含m的代数式表示);
(2)若点B为线段AC的中点,求BO的长;
(3)设AC=x,求当BC与AB的差不小于时整数x的最小值.12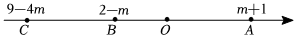 发布:2025/5/24 22:30:1组卷:139引用:4难度:0.4
发布:2025/5/24 22:30:1组卷:139引用:4难度:0.4


