如图，C是ˆAB上的一定点，P是弦AB上的一动点，连接PC，过点A作AQ⊥PC交直线PC于点Q．小石根据学习函数的经验，对线段PC，PA，AQ的长度之间的关系进行了探究．（当点P与点A重合时，令AQ=0cm）
下面是小石的探究过程，请补充完整：
（1）对于点P在弦AB上的不同位置，画图、测量，得到了线段PC，PA，AQ的几组值，如表：
ˆ
AB
| 位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
| PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
| AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
PA
PA
的长度是自变量，PC
PC
的长度和 AQ
AQ
的长度都是这个自变量的函数；（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当AQ=PC时，PA的长度约为
2.8或6.0（答案不唯一）
2.8或6.0（答案不唯一）
cm.（结果保留一位小数）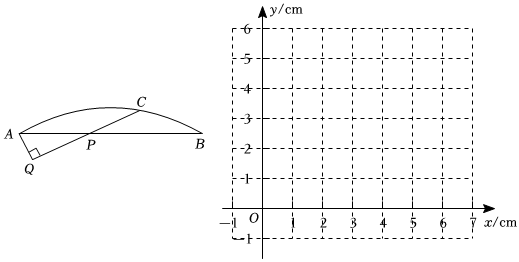
【考点】动点问题的函数图象．
【答案】PA；PC；AQ；2.8或6.0（答案不唯一）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 11:0:4组卷：471引用：5难度：0.4
相似题
-
1．如图，在正方形ABCD中，AB=2，E是AB的中点，动点P从点B开始，沿着边BC，CD匀速运动到D，设点P运动的时间为x,EP=y,那么能表示y与x函数关系的图象大致是（ ）发布：2025/6/17 20:30:2组卷：286引用：3难度：0.7 -
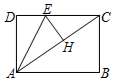2．在矩形ABCD中，对角线AC=4，AC的垂直平分线EH交CD于点E，交AC于点H．设AB=x,CE=y,则y关于x的函数关系用图象大致可以表示为（ ）发布：2025/6/17 17:0:2组卷：592引用：5难度：0.7 -
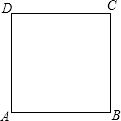3．如图所示，四边形ABCD是边长为4cm的正方形，动点P在正方形ABCD的边上沿着A→B→C→D的路径以1cm/s的速度运动，在这个运动过程中△APD的面积s（cm2）随时间t（s）的变化关系用图象表示，正确的是（ ）发布：2025/6/17 14:30:2组卷：863引用：16难度：0.9
