（1）如图①②，试探究∠1，∠2与∠3，∠4之间的数量关系；
（2）请你用文字语言描述（1）中的关系；
（3）用你发现的结论解决下列问题：如图③，AE，DE分别平分四边形ABCD的外角∠NAD、∠MDA，∠B+∠C=240°，求∠E的度数．
【考点】多边形内角与外角．
【答案】（1）∴∠1+∠2=∠3+∠4；
（2）四边形的任意两个外角的和等于与它们不相邻的两个内角的和；
（3）60°．
（2）四边形的任意两个外角的和等于与它们不相邻的两个内角的和；
（3）60°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/7 8:0:9组卷：294引用：7难度：0.6
相似题
-
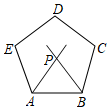1．如图所示，过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P，且∠ABP=60°，则∠APB=度．发布：2025/6/15 20:30:5组卷：1400引用：7难度：0.7 -
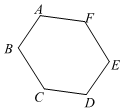2．如图，在六边形ABCDEF中，AF∥CD，AB∥DE，且∠A=120°，∠B=100°，求∠C和∠D的度数．发布：2025/6/15 18:30:1组卷：85引用：6难度：0.6 -
3．如图，在四边形ABCD中，AD∥BC，连接BD，点E在BC边上，点F在DC边上，且∠1=∠2．
（1）求证：EF∥BD；
（2）若DB平分∠ABC，∠A=130°，∠C=70°，求∠CFE的度数．发布：2025/6/15 21:30:1组卷：2291引用：41难度：0.8
