定义，我们习惯把过等腰三角形顶角的顶点引两条射线，使两条射线的夹角为等腰三角形顶角的一半，这样的模型称为半角模型．常见的图形为正方形、正三角形、等腰直角三角形等，在解决“半角模型”的问题时，旋转是一种常用的方法．
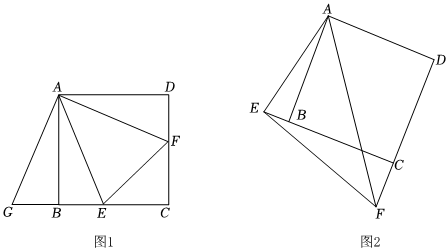
已知，如图1，四边形ABCD是正方形，E，F分别在边BC、CD上，且∠EAF=45°，
（1）在图1中，连接EF，为了证明结论“EF=BE+DF”，小亮将△ADF绕点A顺时针旋转90°后解答了这个问题，请按小亮的思路写出证明过程；
（2）如图2，当∠EAF绕点A旋转到图2位置时，试探究EF与DF、BE之间有怎样的数量关系？
【答案】（1）证明见解析；
（2）EF=DF-BE，证明见解析．
（2）EF=DF-BE，证明见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/23 8:0:8组卷：693引用：4难度：0.4
相似题
-
1．如图，△ABC为等边三角形，AB=8，AD⊥BC，点E为线段AD上的动点，连接CE，以CE为边作等边△CEF，连接DF，则线段DF的最小值为（ ）发布：2025/6/21 2:0:1组卷：1810引用：6难度：0.6 -
2．在△ABC中，∠ACB=90°，点P为△ABC内一点．
（1）如图1，连接PB，PC，将△BCP沿射线CA方向平移，得到△DAE，点B，C，P的对应点分别为点D，A，E，连接CE．如果BP⊥CE，BP=3，AB=6，则CE=．
（2）如图2，连接PA，PB，PC，当AC=BC=8时，求PA+PB+PC的最小值．
发布：2025/6/21 3:0:1组卷：940引用：3难度：0.6 -
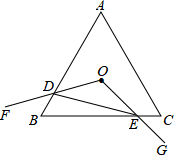3．等边三角形ABC的边长为6，点O是三边垂直平分线的交点，∠FOG=120°，∠FOG的两边OF，OG与AB，BC分别相交于D，E，∠FOG绕O点顺时针旋转时，下列四个结论正确个数是（ ）
①OD=OE；②S△ODE=S△BDE；③S四边形ODBE=；④△BDE周长最小值是92783发布：2025/6/21 3:0:1组卷：4249引用：16难度：0.4
