综合实践课上,刘老师介绍了四点共圆的判定定理:若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆.在实际应用中,如果运用这个定理,往往可以让复杂的问题简单化,以下是小明同学对一道四边形问题的分析,请帮助他补充完整.
特殊情况分析
(1)如图1,正方形ABCD中,点P为对角线AC上一个动点,连接PD,将射线PD绕点P顺时针旋转∠ADC的度数,交直线BC于点Q.
小明的思考如下:
| 连接DQ, ∵AD∥CQ,∠ADC=∠DCQ=90°, ∴∠ACQ=∠DAC,(依据1) ∵∠DPQ=90°, ∴∠DPQ+∠DCQ=180°, ∴点D、P、Q、C共圆, ∴∠PDQ=∠PCQ,∠DQP=∠PCD,(依据2) ∴∠PDQ=∠DQP, ∴DP=QP.(依据3) |
两直线平行,内错角相等
两直线平行,内错角相等
,②依据2应为
同弧所对的圆周角相等
同弧所对的圆周角相等
,③依据3应为
等角对等边
等角对等边
;一般结论探究
(2)将图1中的正方形ABCD改为菱形ABCD,其他条件不变,(1)中的结论是否成立,若成立,请仅以图2的形式证明,若不成立,请说明理由;
结论拓展延伸
(3)若∠ADC=120°,AD=3,当△PQC为直角三角形时,请直接写出线段PQ的长.

【考点】四点共圆.
【答案】两直线平行,内错角相等;同弧所对的圆周角相等;等角对等边
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/26 8:0:9组卷:322引用:4难度:0.2
相似题
-
1.设有边长为1的正方形,试在这个正方形的内接正三角形中找出面积最大的和一个面积最小的,并求出这两个面积(须证明你的论断).
发布:2025/5/28 11:0:1组卷:126引用:1难度:0.7 -
2.定义:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,简称“四点共圆”.我们学过了“圆的内接四边形的对角互补”这一定理,它的逆命题“对角互补的四边形四个顶点共圆”是证明“四点共圆”的一种常用方法.除此之外,我们还经常用“同旁张角相等”来证明“四点共圆”.如图1,在线段AB同侧有两点C,D.连接AD,AC,BC,BD,如果
,那么A,B,C,D“四点共圆”∠C=∠D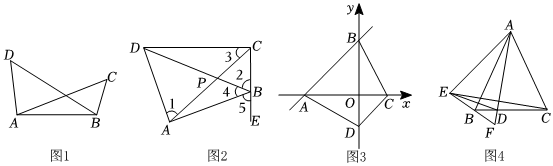
(1)如图2,已知四边形ABCD中,对角线AC、BD相交于点P,点E在CB的延长线上,下列条件:①∠1=∠2;②∠2=∠4:③∠5=:④PA•PC=PB•PD.其中,能判定A,B,C,D“四点共圆”的条件有 :∠ADC
(2)如图3,直线y=x+6与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,点D在y轴负半轴上,若A,B,C,D“四点共圆”,且,求四边形ABCD的面积;∠ADC=105°
(3)如图4,已知△ABC是等腰三角形,AB=AC,点D是线段BC上的一个动点(点D不与点B重合,且BD<CD,连结AD,作点C关于AD的对称点E,连接EB并延长交AD的延长线于F,连接AE,DE.
①求证:A,D,B,E“四点共圆”;
②若AB=2,AD•AF的值是否会发生变化,若不变化,求出其值:若变化,请说明理由.2发布:2025/6/12 1:0:1组卷:698引用:3难度:0.3 -
3.综合与实践
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.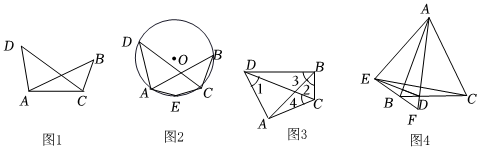
提出问题:
如图1,在线段AC同侧有两点B,D,连接AD,AB,BC,CD,如果∠ABC=∠ADC,那么A,B,C,D四点在同一个圆上.
探究展示:求证:点A,B,C,D四点在同一个圆上.
如图2,作经过点A,C,D的⊙O,在劣弧AC上取一点E(不与A,C重合),连接AE,CE,则∠AEC+∠D=180°
.
(1)请完善探究展示.
(2)如图3,在四边形ABCD中,∠1=∠2,∠3=45°,则∠4的度数为 .
拓展探究:
(3)如图4,已知△ABC是等腰三角形,AB=AC,点D在BC上(不与BC的中点重合),连接AD.作点C关于AD的对称点E,连接EB并延长交AD的延长线于F,连接AB,DE.
①求证:A,D,B,E四点共圆;
②若AB=2,AD•AF的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.2发布:2025/6/1 13:0:1组卷:765引用:2难度:0.3


