阅读以下材料：
通过列表描点我们可以画出y=|x|的图象如图1所示：

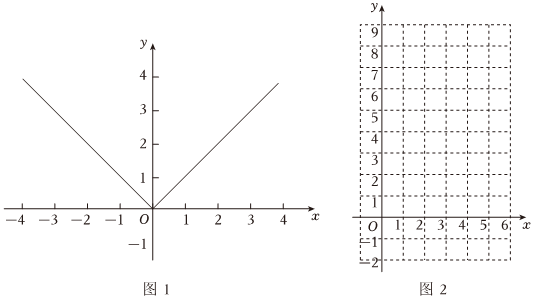
观察图象可以得出以下结论：
x=0时，函数|x|有最小值，最小值是0．
若y随x的增大而增大，x的取值范围是x＞0，若y随x的增大而减少，x的取值范围是x＜0．
提出问题：当x＞0时如何求函数y=x+

1

x

的最大值或最小值？
解决问题：
借鉴我们已有的研究函数的经验，我们利用观察函数的图象探索函数y=x+

1

x

（x＞0）的最大（小）值．
（1）实践操作：填写如表，并用描点法画出函数y=x+

1

x

（x＞0）的图象（图2）：

x	…	1 4	1 3	1 2	1	2	3	4	…
y	…	17 4 17 4	10 3 10 3	5 2 5 2	2 2	5 2 5 2	10 3 10 3	17 4 17 4	…

（2）观察猜想：观察该函数的图象，当x=

1

1

时，函数y=x+

1

x

（x＞0）有最

小

小

值（填“大”或“小”），是

2

2

．若y随x的增大而增大，x的取值范围是

x＞1

x＞1

，若y随x的增大而减少，x的取值范围是

0＜x＜1

0＜x＜1

．
（3）知识能力运用：直接写出函数y=-x-

4

x

（x＞0）当x=

2

2

时，该函数有最

大

大

值（填“大”或“小”），是

-4

-4

．