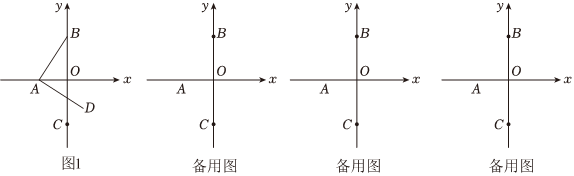
如图，在平面直角坐标系中，已知点B（0，3）、C（0，-3），点A为x轴负半轴上一动点，∠BAO=m°，将线段AB绕点A顺时针旋转n°（0＜n＜360且n≠2m）至AD的位置．
（1）若点A的坐标为（a,0），当n=90时．
①如图1，当a=-1时，点D的坐标为 （2，-1）（2，-1）；
②试用a表示点D的坐标为 （3+a,a）（3+a,a），并用m表示∠ADC的大小为 135°-m°或45°+m°135°-m°或45°+m°；
（2）①当m、n满足条件 当0°＜n°＜90°时，m=45°当0°＜n°＜90°时，m=45°时，∠BDC=135°．
②当m、n满足条件 当135°＜m°＜180°时，n°-2m°=180°当135°＜m°＜180°时，n°-2m°=180°时，∠CBD=90°；
③当m、n满足条件 当0°＜n°＜120°，m°=60°；当120°＜n°＜360°时，80°当0°＜n°＜120°，m°=60°；当120°＜n°＜360°时，80°时，∠BDC+2m°=240°．
【考点】三角形综合题．
【答案】（2，-1）；（3+a，a）；135°-m°或45°+m°；当0°＜n°＜90°时，m=45°；当135°＜m°＜180°时，n°-2m°=180°；当0°＜n°＜120°，m°=60°；当120°＜n°＜360°时，80°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/13 5:0:8组卷：45引用：1难度：0.3
相似题
-
1．如图，AB⊥BC，CD⊥BC，且BC=3cm,AB=1cm,CD=5cm,点P以每秒1cm的速度从点B开始沿射线BC运动，同时点Q在线段CD上由点C向终点D运动．设运动时间为t秒．点Q的速度为xcm/秒．
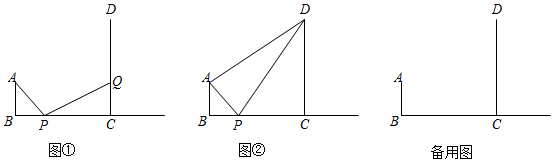
（1）P在线段BC上时，BP=cm,CP=cm.（用含t的代数式表示）
（2）如图①，当点P与点Q经过几秒时，使得△ABP与△PCQ全等？此时，点Q的速度x是多少？（写出求解过程）
（3）如图②，是否存在点P，使得△ADP是等腰三角形？若存在，请直接写出t的值，若不存在，请说明理由．发布：2025/6/14 0:30:2组卷：455引用：3难度：0.4 -
2．已知△ABC是等腰三角形，AC=BC=10，过A作AD⊥BC．
（1）如图1，若△ABC的面积等于40，求BD的长．
（2）如图2，若AB=12，动点M从点B出发以每秒1个单位的速度沿线段BC向点C运动，同时动点N从点C出发以相同的速度沿线段CA向点A运动，当其中一点到达终点时整个运动都停止．设点M运动时间为t（单位：秒）
①若△MDN的边与AB平行，求t的值；
②若点E是AB边的中点，那么在点M运动过程中，△MDE能否成为等腰三角形？若能，请求出t的值；若不能，请说明理由．
发布：2025/6/13 23:0:1组卷：124引用：1难度：0.1 -
3．已知，△ABC是等腰直角三角形，BC=AB，A点在x轴负半轴上，直角顶点B在y轴上，点C在x轴上方．
（1）如图1所示，若A的坐标是（-3，0），点B的坐标是（0，1），求出点C的坐标；
（2）如图2，过点C作CD⊥y轴于D，请直接写出线段OA，CD，OD之间的数量关系；
（3）如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F．问CF与AE有怎样的数量关系？并说明理由．发布：2025/6/13 21:0:2组卷：152引用：4难度：0.2
