请认真完成下列的数学活动．
我们知道，三角形的一个外角等于与它不相邻的两个内角的和，那么三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？

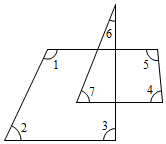
尝试探究
（1）如图①，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间的数量关系．
初步运用
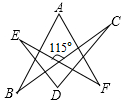
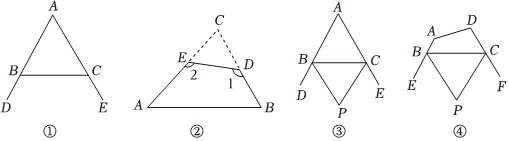
（2）如图②，在△ABC纸片中前去△CED，得到四边形ABDE．若∠2=125°，则∠1-∠C=

55°

55°

．小明联想到了曾经解决的一个问题：如图③，在△ABC中，BP，CP分别平分外角∠DBC，∠ECB，则∠P与∠A之间的数量关系为

∠

P

=

90

°

-

1

2

∠

A

∠

P

=

90

°

-

1

2

∠

A

（请利用上面的结论直接写出答案）．
拓展提升
（3）如图④，在四边形ABCD中，BP，CP分别平分外角∠EBC，∠FCB，设∠A+∠D=α（0°＜α＜360°）．
①试说明∠P与α的数量关系；
②根据α值的情况，请直接判断△BPC的形状（按角分类）．