阅读新知:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个非零常数,这个数列就叫做等比数列.这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).
即:在数列a1,a2,a3,…,an(n为正整数)中,若a2a1=q,a3a2=q,…,则数列a1,a2,a3,…,an(n为正整数)叫做等比数列.其中a1叫数列的首项,a2叫第二项,…,an叫第n项,q叫做数列的公比.例如:数列1,2,4,8,16,…是等比数列,公比q=2.
计算:求等比数列1,3,32,33,…,3100的和.
解:令S=1+3+32+33+⋯+3100,则3S=3+32+33+⋯+3100+3101.
因此3S-S=3101-1,所以S=3101-12.
即1+3+32+33+…+3100=3101-12.
学以致用:
(1)选择题:下列数列属于等比数列的是 CC.
A.1,2,3,4,5
B.2,6,18,21,63
C.56,28,14,7,3.5
D.-11,22,-33,44,-55
(2)填空题:已知数列a1,a2,a3,…an是公比为4的等比数列,若它的首项a1=3,则它的第n项an等于 3×4n-13×4n-1.
(3)解答题:求等比数列1,5,52,53,…,52023的和.
a
2
a
1
a
3
a
2
3
101
-
1
2
3
101
-
1
2
【考点】规律型:图形的变化类;列代数式.
【答案】C;3×4n-1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/3 2:0:8组卷:147引用:1难度:0.5
相似题
-
1.在如图中,每个正方形由边长为1的小正方形组成:
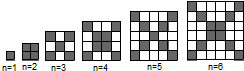
(1)观察图形,请填写下列表格:正方形边长 1 3 5 7 … n(奇数) 黑色小正方形个数
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.正方形边长 2 4 6 8 … n(偶数) 黑色小正方形个数 发布:2025/6/17 23:0:1组卷:330引用:7难度:0.1 -
2.某餐厅中1张餐桌可坐六人,有以下两种摆放方式(如图1和2).
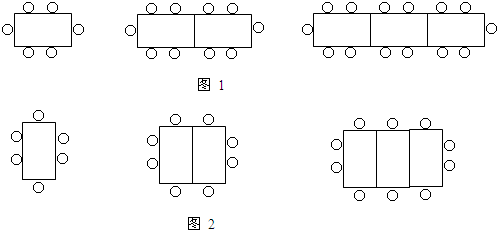
一天中午,餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你应该选择哪种拼接方式来摆餐桌?请说明理由.发布:2025/6/17 21:0:1组卷:163引用:3难度:0.5 -
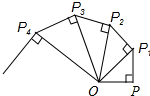 3.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )3发布:2025/6/17 9:30:1组卷:4123引用:15难度:0.7
3.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )3发布:2025/6/17 9:30:1组卷:4123引用:15难度:0.7


