阅读与思考
阅读下列材料，完成后面的任务：
赵爽“弦图”与完全平方公式三国时期吴国的数学家赵爽创建了一幅“弦图”，利用面积法给出了勾股定理的证明．实际上，该“弦图”与完全平方公式有着密切的关系，如图2，这是由8个全等的直角边长分别为a,b,斜边长为c的三角形拼成的“弦图”．由图可知，1个大正方形ABCD的面积=8个直角三角形的面积+1个小正方形PQMN的面积． |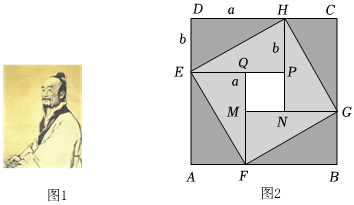
（1）在图2中，正方形ABCD的面积可表示为
（a+b）2
（a+b）2
，正方形PQMN的面积可表示为 （a-b）2
（a-b）2
．（用含a,b的式子表示）（2）根据S正方形ABCD=8S直角三角形+S正方形PQMN，可得（a+b）2，ab,（a-b）2之间的关系为
（a+b）2=4ab+（a-b）2
（a+b）2=4ab+（a-b）2
．（3）根据（2）中的等量关系，解决问题：已知a+b=5，ab=4，求（a-b）2的值．
【答案】（a+b）2；（a-b）2；（a+b）2=4ab+（a-b）2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：947引用：5难度：0.6
相似题
-
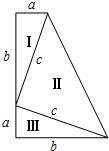1．如图，三个直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一个直角梯形（两底分别为a、b,高为a+b），利用这个图形，小明验证了勾股定理．请你填写计算过程中留下的空格：
S梯形=（上底+下底）•高=12（a+b）•（a+b），即S梯形=12（）①12
S梯形=Ⅰ+Ⅱ+Ⅲ（罗马数字表示相应图形的面积）
=++，即S梯形=（）②12
由①、②，得a2+b2=c2．发布：2025/6/17 20:30:2组卷：305引用：2难度：0.7 -
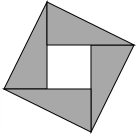2．在北京召开的国际数学家大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形，若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a,较短直角边为b,则a4+b4的值为（ ）发布：2025/6/18 2:30:1组卷：750引用：3难度：0.9 -
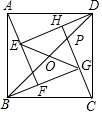3．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接EG，BD相交于点O，BD与HC相交于点P．若GO=GP，则的值是（ ）S正方形ABCDS正方形EFGH发布：2025/6/17 22:0:1组卷：5295引用：33难度：0.6
