观察图，解答下列问题，
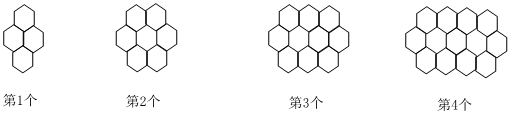
（1）图中的圆圈被折线隔开分成六层，第一层有1个圆圈，第二层有3个圆圈，第三层有5个圆圈，…，第六层有11个圆圈．如果要你继续画下去，第n层有个 （2n-1）（2n-1）圆圈．
（2）某一层上有65个圆圈，这是第 3333层．
（3）数图中的圆圈个数可以有多种不同的方法．比如：前两层的圆圈个数和为（1+3）或22，由此得，1+3=22，同样：由前三层的圆圈个数和得：1+3+5=32，由前四层的圆圈个数和得：1+3+5+7=42，…根据上述规律，从1开始的n个连续奇数之和是多少？用n的代数式把它表示出来．
（4）运用（3）中的规律计算：73+75+77+…+153．
【答案】（2n-1）；33
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/6 1:0:8组卷：263引用：2难度：0.7
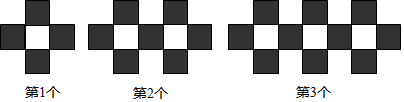
”的个数是 ．
