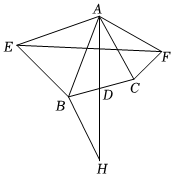
如图，AD为△ABC的中线，分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF，且AE=AB，AF=AC，连接EF，∠EAF+∠BAC=180°．
（1）若∠ABE=63°，∠BAC=45°，求∠FAC的度数；
（2）延长AD至点H，使DH=AD，连接BH，求证：∠ABH+∠BAC=180°；
（3）在（2）的条件下，请直接写出线段EF和线段AD之间的数量关系．
【考点】三角形综合题．
【答案】（1）36°；
（2）见解析；
（3）EF=2AD，理由见解析．
（2）见解析；
（3）EF=2AD，理由见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/27 0:0:1组卷：26引用：1难度：0.2
相似题
-
1．在△ABC中，AB=AC，∠BAC=90°，AD是△ABC的角平分线．
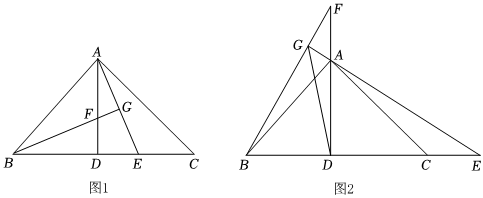
（1）如图1，点E、F分别是线段CD、AD上的点，且DE=DF，AE与BF的延长线交于点G，则AE与BF的数量关系是 ，位置关系是 ；
（2）如图2，点E、F分别在DC和DA的延长线上，且DE=DF，EA的延长线交BF于点G．
①（1）中的结论还成立吗？如果成立，请给出证明：如果不成立，请说明理由；
②连接DG，若DG=4，DE=6，求EG的长．2发布：2025/5/24 11:0:1组卷：397引用：8难度：0.1 -
2．在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．
（1）如图1所示，点M，N分别在线段AD，AB上，且∠BMN=90°，当∠AMN=30°，AB=时，求线段AM的长；6
（2）如图2所示，点E，F分别在AB，AC上，且BE=AF，求证：△DEF是等腰直角三角形；
（3）如图3所示，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB+AN=AM．2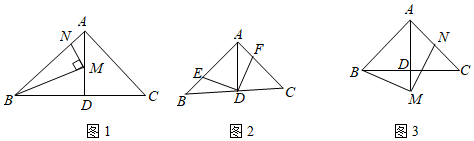
发布：2025/5/24 11:0:1组卷：194引用：3难度：0.2 -
3．如图，在△ABC中，AB=AC=10cm.
（1）如图1，过点A作AH⊥BC于点H，若BC=16cm,AH=6cm,求AB边上的高的长；
（2）如图2，若BC=14cm,点S为AB上一点，且BS=6cm,点P在线段BC上以3cm/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，当点Q的运动速度为多少时，能够使△BPS与△CQP全等？
（3）如图3，点E，F分别在线段BD，DC上，若∠ABD+∠ACD=180°，，∠EAF=12∠BAC
求证：BE+FC=EF．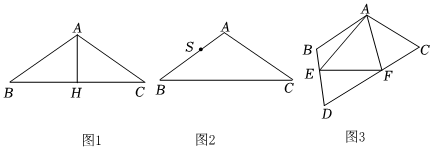
发布：2025/5/24 11:0:1组卷：357引用：4难度：0.1
