探究题：（1）特殊情景：
如图（1），在四边形ABCD中，AB=AD，以点A为顶点作一个角，角的两边分别交BC，CD于点E，F，且∠EAF=12∠BAD，连接EF，若∠BAD=∠B=∠D=90°，探究：线段BE，DF，EF之间的数量关系为：BE+DF=EFBE+DF=EF．
（提示：延长CD到H，使DH=BE，连接AH．）
（2）类比猜想：类比特殊情景，在上述（1）条件下，把“∠BAD=∠B=∠D=90°”改成一股情况“∠B+∠D=180°，”如图（2），小明猜想：线段BE，DF，EF之间的数量关系是否仍然成立？若成立，请证明结论．
（3）解决问题：如图（3），在△ABC中，∠BAC=90°，AB=AC=4，点D，E均在边BC上，且∠DAE=45°，若BD=2，计算DE的长度．
1
2
2
【考点】四边形综合题．
【答案】BE+DF=EF
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/4 8:0:5组卷：779引用：5难度：0.1
相似题
-
1．在人教版八年级上册数学教材P53的数学活动中有这样一段描述：在四边形ABCD中，AD=CD，AB=CB，我们把这种两组邻边分别相等的四边形叫做“筝形”，如图（1）．
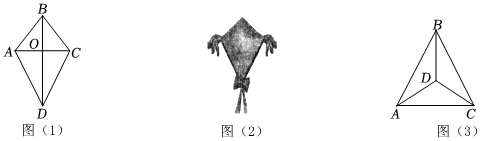
（1）知识应用：小风想要做一个如图（2）所示的风筝，他想先固定中间的“十字架”，再确定四周，从数学的角度看，小风确定“十字架”时应满足什么要求？并证明你的结论．
（2）知识拓展：如图（3）所示，如果D为△ABC内一点，BD平分∠ABC，且AD=CD，试证明：AB=CB．发布：2025/6/9 0:30:2组卷：72引用：1难度：0.2 -
2．矩形ABCD中，∠ACB=30°，△BEF中，∠BEF=90°，∠BFE=30°，BF=
AC，连接FD，点G是FD中点，将△BEF绕点B顺时针旋转α（0°＜α＜360°）．12
（1）如图1，若点B恰好在线段DF延长线上，AB=4，连接EG，求EG的长度；
（2）如图2，若点E恰好落在线段FD上，连接AG，证明：2（GD-GA）=DC；3
（3）如图3，若点E恰好落在线段AB延长线上，点M是线段AD上一点，3AM=DM，N是平面内一点，满足∠MND=∠FDC，已知AB=4，当△DMN是等腰三角形时，直接写出线段MN的长度．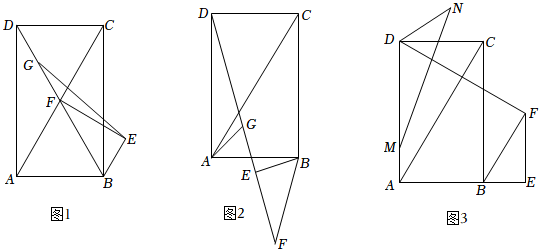
发布：2025/6/9 1:0:1组卷：118引用：1难度：0.1 -
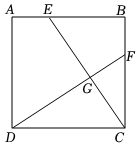3．如图，正方形ABCD中，AE=BF．
（1）求证：△BCE≌△CDF；
（2）求证：CE⊥DF；
（3）若CD=6，且DG2+GE2=41，则BE=．发布：2025/6/8 23:30:1组卷：360引用：3难度：0.6
