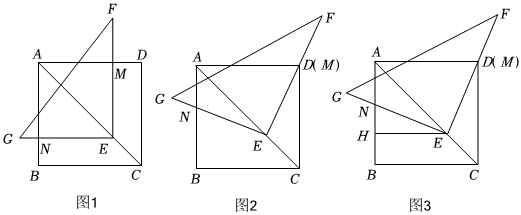
知识探究：如图1，点E是正方形ABCD对角线AC上任意一点，以点E为直角顶点的直角△EFG两边EF，EG分别与AD，AB相交于M点，N点．当EF⊥AD时，请探究EM与EN的数量关系，并说明理由；
拓展探究：当△EFG绕点E顺时针旋转到点M与点D重合时，如图2，请探究EM与EN的数量关系，并说明理由；
迁移运用：在图2的基础上，过点E作EH⊥AB于点H，如图3，证明H是线段BN的中点．
#ZZ01
【答案】知识探究：EM=EN，理由见解答；
拓展探究：EM=EN，理由见解答；
迁移运用：证明过程见解答．
拓展探究：EM=EN，理由见解答；
迁移运用：证明过程见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/3 8:0:9组卷：213引用：1难度：0.4
相似题
-
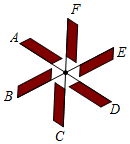1．如图，风车风轮的每个叶片A、B、C、D、E、F在风的吹动下转动到新的位置．则叶片A向方向，转动度后与叶片B重合；转动度后与叶片C重合；转动度后与叶片E重合．由此可知，风车风轮的旋转中心是；最小旋转角是．发布：2025/6/17 21:0:1组卷：33引用：1难度：0.8 -
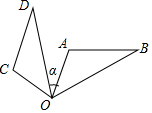2．如图，△OAB绕点O逆时针旋转70°得到△OCD，若∠A=110°，∠D=30°，则∠α的度数是（ ）发布：2025/6/17 20:30:2组卷：161引用：5难度：0.7 -
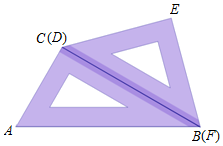3．小明把一副三角板按如图所示叠放在一起，固定三角板ABC，将另一块三角板DEF绕公共顶点B顺时针旋转（旋转的度数不超过180°）．若二块三角板有一边平行，则三角板DEF旋转的度数可能是．发布：2025/6/17 23:30:2组卷：793引用：6难度：0.7
