如图1，∠1、∠2是四边形ABCD的两个不相邻的外角．
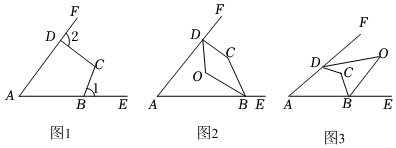
（1）猜想并说明∠1+∠2与∠A、∠C的数量关系；
（2）如图2，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A=58°，∠C=152°，求∠BOD的度数；
（3）如图3，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．
【答案】（1）∠1+∠2=∠A+∠C；
（2）133°；
（3）∠C-∠A=2∠O．
（2）133°；
（3）∠C-∠A=2∠O．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：229引用：4难度：0.7
相似题
-
1．如图①，在△ABC中，AD平分∠BAC，AE⊥BC，∠B=36°，∠C=70°．
（1）求∠DAE的度数；
（2）如图②，若把“AE⊥BC”变成“点F在DA的延长线上，FE⊥BC”，其它条件不变，求∠DFE的度数．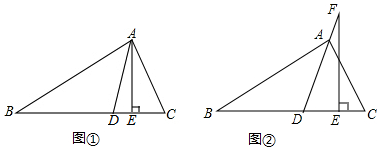
发布：2025/6/14 0:0:1组卷：220引用：3难度：0.7 -
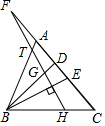2．如图在△ABC中，BD、BE分别是△ABC的高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H．下列结论：①∠DBE=∠F，②2∠BEF=∠BAF+∠C，③∠F=∠BAC-∠C，④∠BED=∠ABE+∠C，其中正确的是（ ）发布：2025/6/14 0:0:1组卷：341引用：3难度：0.6 -
3．△ABC中，∠A=60°，∠C=70°，则∠B的度数是（ ）
发布：2025/6/14 0:0:1组卷：193引用：7难度：0.9
