【积累经验】
(1)萌萌学完全等三角形的知识后,遇到了这样一个问题:如图1,DA⊥AB于点A,CB⊥AB于点B,点E在线段AB上,连接DE,CE,∠DEC=90°,且DE=CE.求证:AD=BE,AE=BC.萌萌发现只需证明△ADEADE≌△BECBEC即可;
【类比应用】
(2)如图2,在平面直角坐标系中,在△ABC中,∠ACB=90°,AC=BC,已知点A的坐标为(0,3),点C的坐标为(2,0),求点B的坐标;
【拓展提升】
(3)如图3,在平面直角坐标系中,点A的坐标为(-6,0),点B为y轴正半轴上一动点,分别以OB,AB为边在第一,第二象限中分别作等腰直角△OBF,等腰直角△ABE,∠ABE=∠OBF=90°,连接EF交y轴于点P,当点B在y轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.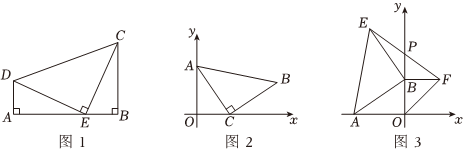
【考点】三角形综合题.
【答案】ADE;BEC
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/16 18:0:2组卷:251引用:2难度:0.3
相似题
-
1.已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是大于14的偶数.
①求c的长;
②判断△ABC的形状.发布:2025/6/16 22:30:4组卷:117引用:2难度:0.4 -
2.在△ABC中,∠ACB=2∠B.
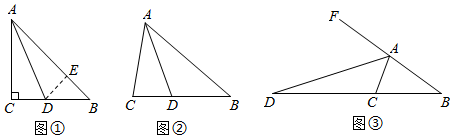
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证:CD=DE=;AC+CD=;(请直接写出结论,不用证明.)
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,模仿题(1)的思路,求证:AB=AC+CD;
(3)如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.发布:2025/6/16 18:30:2组卷:191引用:1难度:0.4 -
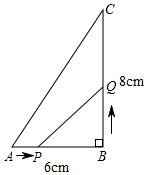 3.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
3.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
【思考】如果点P,Q分别从点A,B同时出发,经过几秒,△PBQ的面积等于8cm2?
【探究】如果点P,Q分别从点A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,说明理由.
【拓展】若点P沿射线AB方向从点A出发,以1cm/s的速度移动,点Q沿射线CB方向从点C出发,以2cm/s的速度移动,点P,Q同时出发,则经过几秒,△PBQ的面积为1cm2?发布:2025/6/16 21:0:1组卷:233引用:1难度:0.3


