如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E与点A不重合时，过点E作EF⊥AD于点F，作GE∥AD交AC于点G，过点G作射线AD垂线段GH，垂足为点H，得到矩形EFHG，设点E的运动时间为t秒．
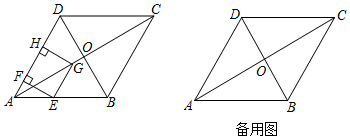
（1）求点H与点D重合时t的值；
（2）设矩形EFHG与菱形ABCD重叠部分图形的面积为S，求S与t之间的函数关系式；
（3）设矩形EFHG的对角线EH与FG相交于点O′，
①当OO′∥AD时，t的值为 44；
②OO′⊥AD时，求出t的值．
【考点】四边形综合题．
【答案】4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：796引用：4难度：0.4
相似题
-
1．（1）如图1，纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCF的位置，拼成四边形AEFD，则四边形AEFD的形状为 ．
A．平行四边形 B．菱形 C．矩形 D．正方形
（2）如图2，在（1）中的四边形纸片AEFD中，在EF上取一点G，使EG=4，剪下△AEG，将它平移至△DFH的位置，拼成四边形AGHD．
①求证：四边形AGHD是菱形；
②求四边形AGHD的两条对角线的长．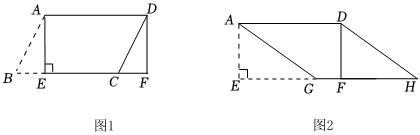
发布：2025/6/7 20:0:2组卷：22引用：2难度：0.2 -
2．如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a,0），点C的坐标为（0，b），且a、b满足，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-A-B-C-O的线路移动．a-4+|b-6|=0
（1）a=，b=，点B的坐标为 ；
（2）①当点P移动3秒时，此时点P的坐标 ；
②当点P移动6秒时，请在图中点出点P的位置，并求出点P的坐标；
（3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．发布：2025/6/7 19:30:2组卷：155引用：1难度：0.2 -
3．在矩形ABCD中，AB=3，AD=5，经过折叠使点A落在BC边上的点E处，折痕为PQ．当点E在BC边上移动时，折痕的端点P，Q也随之移动．规定点P、Q分别在AB，AD上移动．
（1）当点A落在图1中E点处，如果PA=2，求BE的长为多少？
（2）当点E恰好是BC的中点时，AP和DQ的长分别是多少？
（3）点E在BC边上可移动的最大距离是多少？发布：2025/6/7 19:30:2组卷：70引用：2难度：0.1
