【复习旧知】结合数轴与绝对值的知识回答下列问题：
数轴上表示4和1的两点之间的距离是3；而|4-1|=3；表示-3和2两点之间的距离是5；而|-3-2|=5；表示-4和-7两点之间的距离是3；而|-4-（-7）|=3．
一般地，数轴上表示数m和数n的两点之间的距离公式为|m-n|．
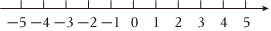
（1）数轴上表示数-4的点与表示-1的点之间的距离为 33．
【探索新知】
如图①，我们在“格点”直角坐标系上可以清楚看到：要找AB或DE的长度，显然是化为求Rt△ABC或Rt△DEF的斜边长．
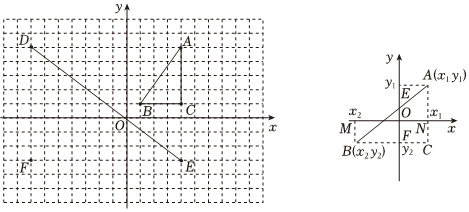
下面：以求DE为例来说明如何解决．
从坐标系中发现：D（-7，5），E（4，-3）．所以DF=|5-（-3）|=8，EF=|4-（-7）|=11，所以由勾股定理可得：DE=82+112=185．
（2）在图②中：设A（x1，y1），B（x2，y2），试用x1，y1，x2，y2表示：AC=y1-y2y1-y2，BC=x1-x2x1-x2，AB=（x1-x2）2+（y1-y2）2（x1-x2）2+（y1-y2）2．
得出的结论被称为“平面直角坐标系中两点间距离公式”．
【学以致用】请用此公式解决如下题目：
（3）已知A（-2，3）、B（4，-5），试求A、B两点间的距离．
（4）已知一个三角形各顶点坐标为A（-1，1）、B（-3，3）、C（2，4），请判定此三角形的形状，并说明理由．
DE
=
8
2
+
1
1
2
=
185
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
【考点】三角形综合题．
【答案】3；y1-y2；x1-x2；
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/6 2:0:1组卷：172引用：1难度：0.2
相似题
-
1．（1）阅读理解：
如图1，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE=AD，连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是；
（2）问题解决：如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．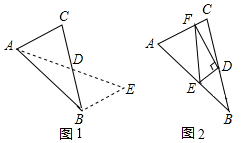
发布：2025/6/17 11:0:1组卷：624引用：7难度：0.4 -
2．如图，三角形ABO的三个顶点的坐标分别为O（0，0），A（5，0），B（2，4）．
（1）求三角形OAB的面积；
（2）若O，B两点的位置不变，点M在x轴上，则点M在什么位置时，三角形OBM的面积是三角形OAB的面积的2倍？
（3）若O，A两点的位置不变，点N由点B向上或向下平移得到，则点N在什么位置时，三角形OAN的面积是三角形OAB的面积的2倍？发布：2025/6/17 6:30:2组卷：331引用：2难度：0.3 -
3．如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
（1）求证：AD=BE；
（2）求∠AEB的度数；
（3）探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM⊥DE于点M，连接BE．
①∠AEB的度数为 °；
②线段DM，AE，BE之间的数量关系为 ．（直接写出答案，不需要说明理由）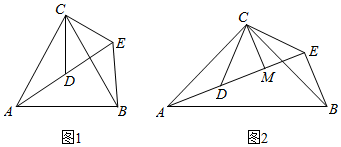
发布：2025/6/17 6:0:2组卷：365引用：3难度：0.6
