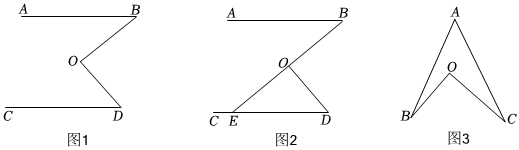
（1）如图1，AB∥CD．写出∠BOD与∠B，∠D之间的数量关系，并说明理由；
（2）如图2，在（1）的条件下，延长BO交CD于点E，若∠CEO=5∠OED，∠BOD=75°，求∠D的度数；
（3）如图3，结合（1）中的结论，探究∠BOC与∠A，∠ABO，∠ACO之间的数量关系，并说明理由．
【考点】三角形综合题．
【答案】（ 1 ）∠BOD=∠B+∠D，理由见解析；
（2）45°；
（3）∠BOD=∠B+∠ACO+∠A，理由见解析．
（2）45°；
（3）∠BOD=∠B+∠ACO+∠A，理由见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/26 8:0:9组卷：157引用：2难度：0.3
相似题
-
1．如图，在△ABC中，∠ACB=90°，CA=CB，∠MCN=45°，射线CM交直线AB于点P，过点A作AD⊥CM于点D，直线AD交直线CN于点E，连接BE．
（1）当点P在线段AB上时，如图①，求证：AD+BE=DE；
（2）当点P在BA的延长线上时，如图②；当点P在AB的延长线上时，如图③，线段AD，DE，BE之间又有怎样的数量关系？直接写出你的猜想，不必证明．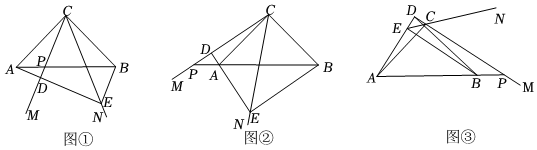
发布：2025/5/25 19:30:2组卷：79引用：1难度：0.3 -
2．已知：在△ABC中，AB=AC，∠BAC=120°，点F是线段BC上一点，D、E是射线AF上两点，且∠ADB=∠BAC，∠AEC=60°．
（1）如图1，
①填空：∠BAE ∠ACE；（填“＞”或“=”或“＜”）
②判定三条线段AD，BD，CE的数量关系，并说明理由；
（2）若∠DBC=15°，则直接写出的值．FCBF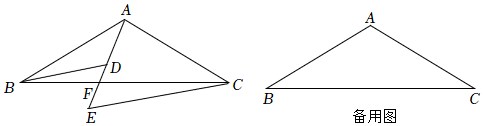
发布：2025/5/25 17:30:1组卷：278引用：3难度：0.1 -
3．如图①，在△ABC中，∠ABC=90°，过点B作直线BD交边AC于点D，过点A作AE⊥BD，垂足为点E，过点C作CF⊥BD，垂足为点F，点O为AC的中点，连结OE、OF．
【证明推断】求证：OE=OF．
小明给出的思路：先分别延长EO、CF交于点M，再证明△AEO≌△CMO．请你根据小明的思路完成证明过程．
【拓展应用】如图②，当BC=4AB，∠DBC=45°时，解决下列问题：
（1）∠EFO的大小为 度．
（2）的值为 ．ODOC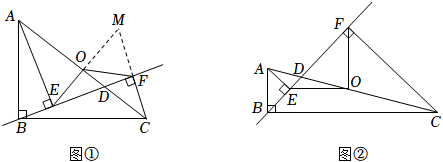
发布：2025/5/25 18:0:1组卷：179引用：2难度：0.4
