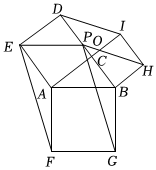
欧几里得《几何原本》中给出一种证明勾股定理的方法：“直角三角形斜边上正方形的面积等于两直角边上两个正方形的面积之和”．如图，△ABC中，∠ACB=Rt∠，四边形ACDE、四边形BAFG和四边形BHIC都是正方形，过点E作AB的平行线交DC于点P，连结EF，PG，PH．若四边形EFGP的面积是四边形DPHI的面积的5倍，设PH与CI交于点O，则POPH的值是（ ）
PO
PH
【考点】相似三角形的判定与性质；勾股定理的证明．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/16 8:0:9组卷：878引用：2难度：0.3
相似题
-
1．如图，在梯形ABCD中，AB∥CD，对角线AC、BD相交于点O，如果S△AOB=2S△AOD，AC=10，那么OC的长是．发布：2025/1/28 8:0:2组卷：107引用：1难度：0.4 -
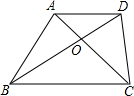2．如图，梯形ABCD中AD∥BC，对角线AC、BD交于0点，△AOD与△DOC的面积之比为3：7，则AD：BC=．发布：2025/1/28 8:0:2组卷：39引用：1难度：0.7 -
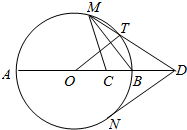3．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连接MC，MB，OT．
（Ⅰ）求证：DT•DM=DO•DC；
（Ⅱ）若∠DOT=60°，试求∠BMC的大小．发布：2025/1/28 8:0:2组卷：364引用：1难度：0.3
