（1）方法回顾
在学习三角形中位线时探索三角形中位线的性质，思路如下：
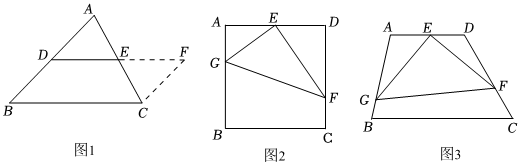
第一步添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF=DE，连接
CF；
第二步证明△ADE≌△CFE，再证四边形DBCF是平行四边形，从而得到中位线DE与BC的数量关系是 DE∥BC，BC=2DEDE∥BC，BC=2DE；（直接填写结果）
（2）问题解决
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若 AG=2，DF=3，∠GEF=90°，求GF的长．
（3）拓展研究
如图3，在四边形ABCD中，∠A=105°，∠D=120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG=2，DF=3，∠GEF=90°，求GF的长．
AG
=
2
2
【考点】四边形综合题．
【答案】DE∥BC，BC=2DE
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/5 8:0:9组卷：234引用：1难度：0.2
相似题
-
1．在人教版八年级上册数学教材P53的数学活动中有这样一段描述：在四边形ABCD中，AD=CD，AB=CB，我们把这种两组邻边分别相等的四边形叫做“筝形”，如图（1）．
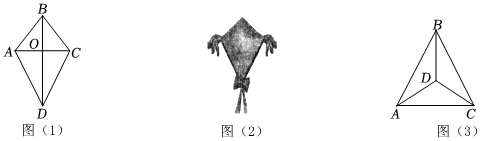
（1）知识应用：小风想要做一个如图（2）所示的风筝，他想先固定中间的“十字架”，再确定四周，从数学的角度看，小风确定“十字架”时应满足什么要求？并证明你的结论．
（2）知识拓展：如图（3）所示，如果D为△ABC内一点，BD平分∠ABC，且AD=CD，试证明：AB=CB．发布：2025/6/9 0:30:2组卷：72引用：1难度：0.2 -
2．（1）如图1，在四边形ABCD中，∠B=∠C=90°，点E是边BC上一点，AB=EC，BE=CD，连接AE、DE．判断△AED的形状，并说明理由；
（2）在平面直角坐标系中，已知点A（2，0），点B（5，1），点C在第一象限内，若△ABC是等腰直角三角形，求点C的坐标；
（3）如图2，在平面直角坐标系中，已知点A（0，1），点C是x轴上的动点，线段CA绕着点C按顺时针方向旋转90°至线段CB，连接BO、BA，则BO+BA的最小值是 ．
发布：2025/6/8 23:30:1组卷：886引用：3难度：0.3 -
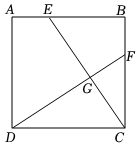3．如图，正方形ABCD中，AE=BF．
（1）求证：△BCE≌△CDF；
（2）求证：CE⊥DF；
（3）若CD=6，且DG2+GE2=41，则BE=．发布：2025/6/8 23:30:1组卷：360引用：3难度：0.6
