【数学概念】
我们把存在内切圆与外接圆的四边形称为双圆四边形．例如，如图①，四边形ABCD内接于⊙M，且每条边均与⊙P相切，切点分别为E，F，G，H，因此该四边形是双圆四边形．
【性质初探】
（1）双圆四边形的对角的数量关系是 互补互补，依据是 圆内接四边形的对角互补圆内接四边形的对角互补．
（2）直接写出双圆四边形的边的性质．（用文字表述）
（3）在图①中，连接GE，HF，求证GE⊥HF．
【揭示关系】
（4）根据双圆四边形与四边形、平行四边形、矩形、菱形、正方形的关系，在图②中画出双圆四边形的大致区域，并用阴影表示．
【特例研究】
（5）已知P，M分别是双圆四边形ABCD的内切圆和外接圆的圆心，若AB=2，BC=4，∠B=90°，则PM的长为 5353．
5
3
5
3
【考点】圆的综合题．
【答案】互补；圆内接四边形的对角互补；
5
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/24 1:0:8组卷：171引用：4难度：0.1
相似题
-
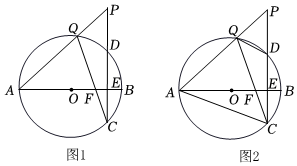1．如图，⊙O的直径AB垂直于弦CD于点E，AB=10，CD=6，点P是CD延长线上异于点D的一个动点，连结AP交⊙O于点Q，连结CQ交AB于点F，则点F的位置随着点P位置的改变而改变．
（1）如图1，当DP=4时，求tan∠P的值；
（2）如图2，连结AC，DQ，在点P运动过程中，设DP=x,．S△QACS△QDC=y
①求证：∠ACQ=∠CPA；
②求y与x之间的函数关系式．发布：2025/6/13 1:0:1组卷：2067引用：6难度：0.3 -
2．如图，AB为⊙O直径，点C为⊙O上任意一点，连接OC，过点A作OC的平行线，交⊙O于点D，连接CD．
（1）如图1，求证：CO平分∠BCD；
（2）如图2，点F在线段DO的延长线上，连接AF交CD于E，若AE=EF，求证：DA=DF；
（3）如图3，在（2）条件下，延长AF交线段BC于点G，若CD=12，BG=4，求AF的长．发布：2025/6/13 1:30:1组卷：79引用：2难度：0.2 -
3．如图，四边形ABCD内接于⊙O，AC平分∠BCD．
（1）如图1，求证：AB=AD；
（2）如图2，点E在弧AD上，弧CE=弧BC，延长CD、AE交于点F，求证：AF=AD．
（3）在（2）的条件下，如图3，连接ED并延长ED交AC延长线于点P，连接PF，若PF=AF=4，PE=10，求⊙O的半径．5
发布：2025/6/13 2:0:4组卷：103引用：1难度：0.3
