已知抛物线y=x2-2ax+m.
（1）当a=2，m=-5时，求抛物线的最值；
（2）当a=2时，若该抛物线与坐标轴有两个交点，把它沿y轴向上平移k个单位长度后，得到新的抛物线与x轴没有交点，请判断k的取值情况，并说明理由；
（3）当m=0时，平行于y轴的直线l分别与直线y=x-（a-1）和该抛物线交于P，Q两点．若平移直线l,可以使点P，Q都在x轴的下方，求a的取值范围．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/1 15:0:2组卷：863引用：4难度：0.3
相似题
-
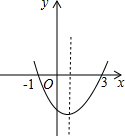1．如图为二次函数y=ax2+bx+c的图象，在下列说法中：
①abc＞0；
②方程ax2+bx+c=0的根为x1=-1，x2=3；
③a+b+c＞0；
④当x＞1时，y随着x的增大而增大．
正确的说法个数是（ ）发布：2025/5/27 13:30:1组卷：614引用：8难度：0.9 -
2．抛物线y=ax2+bx+c的图象大致如图所示，有下列说法：①a＞0，b＜0，c＜0；②函数图象可以通过抛物线y=ax2向下平移，再向左平移得到；③直线y=ax+b必过第一、二、三象限；④直线y=ax+c与此抛物线有两个交点，其中正确的有（ ）个．发布：2025/5/28 0:30:1组卷：99引用：5难度：0.9 -
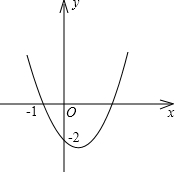3．二次函数y=ax2+bx+c的图象如图所示，那么a+b+c的取值范围是（ ）发布：2025/5/27 18:0:1组卷：1121引用：4难度：0.5
