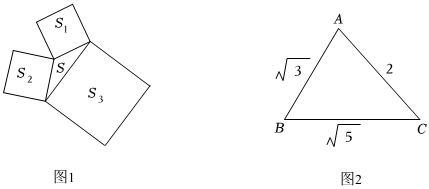
海伦是古希腊数学家,约公元62年左右活跃于亚历山大,年青时海伦酷爱数学,他的代表作《量度论》主要是研究面积、体积和几何分比问题,其中一段探究三角形面积的方法翻译如下:如图1,设三角形面积为S,以三角形各边为边向外作正方形,三个正方形的面积分别记作S1、S2、S3,定义:S=S1+S2+S32;S1'=S-S1;S2'=S-S2;S3'=S-S3;FS=S1'×S2′+S2'×S3'+S3'×S1',经研究发现,FS=4S2.如:三角形三条边分别为13、14、15,则S1=169,S2=196,S3=225,S=295,S1'=126;S2′=99;S3′=70;Fs=28224,所以S2=28224÷4=7056=842,故三角形的面积S=84.
(1)如图2,在△ABC中,S1=3,S2=4,S3=5,则S=66,Fs=1111,△ABC的面积S=112112.
(2)在△DEF中,若S1′=x-3;S2′=x+3;S3′=5-x.
①若△DEF的面积S=3,求x的值;
②若△DEF的面积是否存在最大值?如果存在,请直接写出此时外接圆的直径,如果不存在,请简要说明理由.
S
=
S
1
+
S
2
+
S
3
2
S
S
S
S
S
11
2
11
2
3
【答案】6;11;
11
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/26 17:0:2组卷:61引用:1难度:0.7
相似题
-
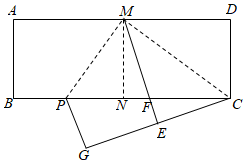 1.如图,在矩形ABCD中,AD=2AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=2MP;④BP=62AB;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )22发布:2025/6/17 18:30:1组卷:2450引用:10难度:0.4
1.如图,在矩形ABCD中,AD=2AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=2MP;④BP=62AB;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )22发布:2025/6/17 18:30:1组卷:2450引用:10难度:0.4 -
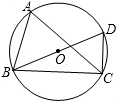 2.如图,△ABC内接于⊙O,BD是⊙O的直径,∠CBD=21°,则∠A的度数为.发布:2025/6/17 18:30:1组卷:1312引用:16难度:0.8
2.如图,△ABC内接于⊙O,BD是⊙O的直径,∠CBD=21°,则∠A的度数为.发布:2025/6/17 18:30:1组卷:1312引用:16难度:0.8 -
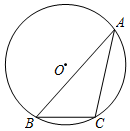 3.如图,⊙O是△ABC的外接圆,半径为2cm,若BC=2cm,则∠A的度数为( )发布:2025/6/17 18:30:1组卷:3787引用:29难度:0.5
3.如图,⊙O是△ABC的外接圆,半径为2cm,若BC=2cm,则∠A的度数为( )发布:2025/6/17 18:30:1组卷:3787引用:29难度:0.5


