某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x=25时，y=550；当x=30时y=500．物价部门规定，该商品的销售单价不能超过52元/件．
（1）求出y与x的函数关系式；
（2）问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？
（3）当销售单价定为多少元时，商家销售该商品每天获得的利润最大，并求出最大利润．
【答案】（1）y=-10x+800（0＜x≤52）；
（2）销售单价定为40元/件时，工艺厂试销该工艺品每天获得的利润8000元；
（3）当销售单价定为50元时，商家销售该商品每天获得的利润最大，其最大利润为9000元．
（2）销售单价定为40元/件时，工艺厂试销该工艺品每天获得的利润8000元；
（3）当销售单价定为50元时，商家销售该商品每天获得的利润最大，其最大利润为9000元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/5 6:0:3组卷：204引用：6难度：0.6
相似题
-
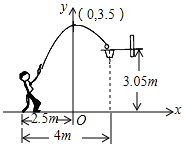1．一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m,然后准确落入篮筐内．已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中，下列说法正确的是（ ）发布：2025/6/17 17:30:2组卷：937引用：21难度：0.5 -
2．用承重指数W衡量水平放置的长方体木板的最大承重量．实验室有一些同材质同长同宽而厚度不一的木板，实验发现：木板承重指数W与木板厚度x（厘米）的平方成正比，当x=3时，W=3．
（1）求W与x的函数关系式．
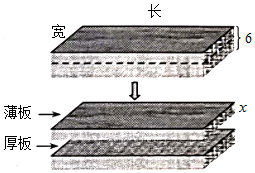
（2）如图，选一块厚度为6厘米的木板，把它分割成与原来同长同宽但薄厚不同的两块板（不计分割损耗）．设薄板的厚度为x（厘米），Q=W厚-W薄．
①求Q与x的函数关系式；
②x为何值时，Q是W薄的3倍？[注：（1）及（2）中的①不必写x的取值范围]发布：2025/6/17 17:30:2组卷：2347引用：9难度：0.7 -
3．某种商品每件进价为20元，调查表明：在某段时间内若以每件x元（20≤x≤30，且x为整数）出售，可卖出（30-x）件，若使利润最大，则每件商品的售价应为元．
发布：2025/6/17 17:30:2组卷：2391引用：10难度：0.7
