综合与实践
综合与实践课上，同学们以“四边形的折叠”为主题开展数学活动．
操作判断
（1）操作一：如图1，将正方形纸片ABCD沿对角线AC折叠，然后将纸片展开；
操作二：依次将边AB，CD折到对角线AC上，折痕分别为AE，CG，使点B，D分别落在对角线AC上的点F，H处，将纸片展开，连接EH，FG．
根据以上操作，易得出结论：四边形EFGH的形状是 平行四边形平行四边形．
迁移探究
（2）如图2，将正方形纸片换成矩形纸片，按照（1）中的方式操作，继续探究．
①小明认为此时四边形EFGH的形状仍然符合（1）中的结论，你认为小明的说法正确吗？请说明理由；
②小亮认为可以通过改变矩形AB与BC的比值，让四边形EFGH成为菱形，你认为小亮说法正确吗？请简述理由．
拓展应用
（3）在（2）的条件下，若AB=6，当F，H分别是线段AC的三等分点时，请直接写出四边形EFGH的面积．
【考点】四边形综合题．
【答案】平行四边形
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/15 8:0:9组卷：200引用：2难度：0.4
相似题
-
1．已知正方形ABCD中，点E是线段BC上的动点（不包含端点），以AE为直角边在直线BC的上方作等腰直角三角形AEF，∠AEF=90°．
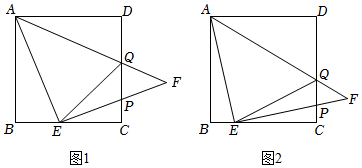
（1）如图1，若BE=DQ，请直接写出图中与∠AEQ相等的两个角；
（2）如图2，点E在BC上运动的过程中，图中有几个角始终与∠AEQ相等？请选择其中的一个予以证明；
（3）若正方形ABCD的边长为3，BE=x,设点P到直线EQ的距离为y,求y与x之间的函数关系式，并求出y的最大值．发布：2025/5/23 15:30:2组卷：526引用：2难度：0.3 -
2．在菱形ABCD中，
，∠ABC=60°，点E是对角线BD上的一动点，以AE为边向右作等边三角形AEF，连结CF．AB=23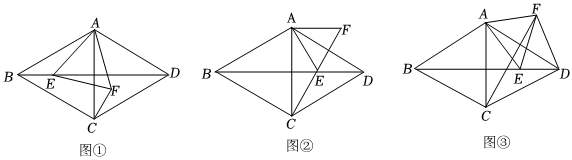
（1））如图①，当点F在菱形内部时，求证：△ABE≌△ACF．
（2）如图②，当C、E、F三点在一条直线上时，AE=．
（3）如图③，当时，连结DF，四边形AEDF的面积=．DE=14BD发布：2025/5/23 15:30:2组卷：195引用：1难度：0.2 -
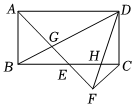3．如图，在矩形ABCD中，AE平分∠BAD交射线BC于点E，过点C作CF⊥AE交射线AE于点F，连结BD交AE于点G，连结DF交射线BC于点H．
（1）当AB＜AD时，
①求证：BE=CD；
②猜想∠BDF的度数，并说明理由．
（2）若时，求tan∠CDF的值（用含k的代数式表示）．ABAD=k发布：2025/5/23 15:30:2组卷：447引用：3难度：0.1
