我们把形如

a

n

x

n

+

a

n

-

1

x

n

-

1

+

…

+

a

1

x

+

a

0

（

a

n

≠

0

）

的整式称为关于x的一元n次多项式，记作f（x），g（x）…将整数的带余除法类比到一元多项式，我们可类似地得到带余式的大除法，其关系式为：f（x）=g（x）•q（x）+r（x），其中f（x）表示被除式，g（x）表示除式，q（x）表示商式，r（x）表示余式，且r（x）的次数小于g（x）的次数．
我们来举个例子对比多项式除法和整数除法，如图左式中，13579除以112，商为121，余数为27：而如下右式中，多项式x⁴+3x³+5x²+7x+9除以x²+x+2，商式为x²+2x+1，余式为2x+7．

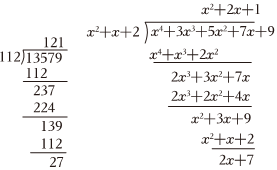
请根据以上材料，解决下面的问题：
（1）多项式2x⁴+3x²-x+2除以x²-2x+3，请补全下面的计算式；

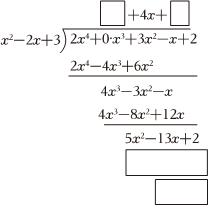
所以，2x⁴+3x²-x+2除以x²-2x+3所得的商式为

2x²+4x+5

2x²+4x+5

，余式为

-3x-13

-3x-13

．
（2）若多项式x⁴+px²+x+q除以x²+3x+4所得的余式为x-1，求p²+q²的值．