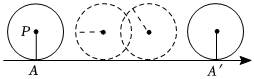
已知数轴上A、B、C三个点对应的数分别是a,b,c,且|a-12|+|b-5|+(c+5)2=0;动点P从C点出发,向右移动,速度为1个单位长度/秒,设移动时间为t秒.
(1)求a,b,c的值;
(2)以AB为长,BO为宽,作出长方形EFMN,其中M与A重合,N与B重合(如图所示),将这个长方形总绕着右边的端点不断滚动(无滑动),求E点第3次落在数轴上对应的数字;
(3)将(2)中的长方形EFMN,M与A重合,N与B重合时开始计时,该长方形以2个单位长度/秒的速度向左移动.当N点与C点重合时,立即返回向右移动,当M点与A点重合时,立即返回向左移动,N点再次到达C点时停止,整个过程中速度保持不变,当P点与M点相遇时,求t的值.

【答案】(1)a=12,b=5,c=5;
(2)E点第3次落在数轴上对应的数字是72;
(3)当t为 秒时,P点与M点相遇.
(2)E点第3次落在数轴上对应的数字是72;
(3)当t为
37
3
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/23 8:0:8组卷:62引用:2难度:0.5