【问题背景】（1）如图1，△ABC中，∠BED=∠BCA，求证：BDAB=BEBC．
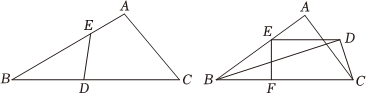
【问题探究】（2）如图2，△ABC中，∠A=90°，BD平分∠ABC，CD⊥BD于点D，过点D作BC的平行线交AB于点E，作EF⊥BC于点F，猜想EF与已有的哪条线段的一半相等，并加以证明；
【问题拓展】（3）在（2）上述条件下，当FC=AC时，直接写出∠BCD的正切值tan∠BCD．
BD
AB
=
BE
BC
【考点】相似形综合题．
【答案】（1）证明过程见解析；
（2），证明过程见解析；
（3）tan∠BCD=3．
（2）
EF
=
1
2
AC
（3）tan∠BCD=3．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/9 8:0:9组卷：141引用：2难度：0.5
相似题
-
1．如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若△ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E（点D不与点B重合，点E不与点C重合）．设BE=m,CD=n.
（1）求证：△ABE∽△DCA；
（2）求m与n的函数关系式，直接写出自变量n的取值范围；
（3）以△ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系（如图2）．在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD2+CE2=DE2．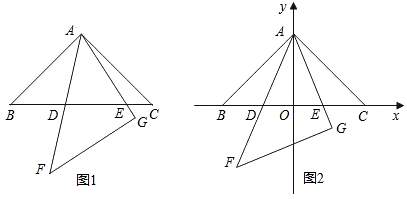
发布：2025/6/23 22:0:2组卷：99引用：2难度：0.5 -
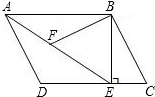2．如图，在平行四边形ABCD中，过点B作BE⊥CD于E点，连接AE，F为AE上一点，且∠BFE=∠C．
（1）求证：△ABF∽△EAD；
（2）若AB=4，∠BAE=30°，求AE的长；
（3）在（1）（2）的条件下，若AD=3，求BF的长．发布：2025/6/23 15:30:2组卷：181引用：5难度：0.1 -
3．在△ABC中，AC=25，AB=35，
，点D为边AC上一点，且AD=5，点E、F分别为边AB上的动点（点F在点E的左边），且∠EDF=∠A．设AE=x,AF=y.tanA=43
（1）如图1，当DF⊥AB时，求AE的长；
（2）如图2，当点E、F在边AB上时，求y关于x的函数关系式，并写出函数的定义域；
（3）连接CE，当△DEC和△ADF相似时，求x的值．
发布：2025/6/24 1:30:2组卷：510引用：2难度：0.5
