数学课外学习小组在一次学习中遇到下面的问题：
如图1：有公共顶点的两个△ABC和△ADE，满足AB=AC，AD=AE，∠BAC=∠DAE，小伟发现如果连接BD，CE，如图2，会得到一对全等三角形，小明说，连接ED并延长和BC交于点F，如果∠ADB=90°，那么F就一定是BC的中点如图3．
（1）按照小伟的说法，找到全等三角形，并证明．
（2）小明的说法是否正确，若正确证明结论，若不正确说明理由．
【考点】全等三角形的判定与性质．
【答案】（1）△ABD≌△ACE，证明见解析；
（2）小明的说法是正确的，证明见解析．
（2）小明的说法是正确的，证明见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 4:0:8组卷：73引用：1难度：0.5
相似题
-
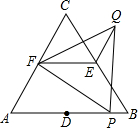1．如图，△ABC和△FPQ均是等边三角形，点D、E、F分别是△ABC三边的中点，点P在AB边上，连接EF、QE．若AB=6，PB=1，则QE=．发布：2025/6/18 17:30:1组卷：3576引用：43难度：0.7 -
2．如图，在△ABC中，∠ABC=45°，AC=5，F是高AD和BE的交点，则BF的长是（ ）发布：2025/6/18 17:0:1组卷：2254引用：7难度：0.9 -
3．如图，已知AB⊥AD，AC⊥AE，AB=AD，AC=AE，BC分别交AD、DE于点G、F，AC与DE交于点H．
求证：
（1）△ABC≌△ADE；
（2）BC⊥DE．发布：2025/6/18 17:0:1组卷：1735引用：17难度：0.5
