如图，△ABC是边长为6厘米的等边三角形，点D从C点出发沿C→A方向在线段CA上以a厘米/秒的速度运动，点E从B点出发沿B→C方向在射线BC上以b厘米/秒的速度运动，D、E两点同时出发，运动时间为t秒，当点D到达点A后，D、E两点停止运动连接AE、BD，AE交BD（或BD延长线）于点F．
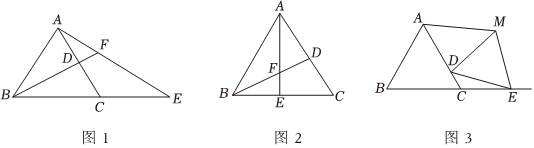
（1）如图1，若a=1，b=4，t=3，则∠AFB=60°60°；
（2）如图2，若a=b=1，当AF=BF时，求t的值；
（3）如图3，点D在线段CA上运动，但不与端点A、C重合，当点E运动到点C右侧时，连接DE，以DE为边向右上方作等边△DEM，连接AM，请直接写出S四边形DCEM S△ADM的值（结果用含a,b,t的式子表示）．
S
四边形
DCEM
S
△
ADM
【考点】三角形综合题．
【答案】60°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/21 1:0:8组卷：37引用：1难度：0.3
相似题
-
1．现有一副直角三角板（角度分别为30°、60°、90°和45°、45°、90°）如图（1）放置，其中一块三角板的直角边AC垂直于数轴，AC的中点过数轴的原点O，AC=8，斜边AB交数轴于点G，点G对应数轴上的数是4；另一块三角板的直角边AE交数轴于点F，斜边AD交数轴于点H．
（1）如果△AGH的面积是10，△AHF的面积是8，则点F对应数轴上的数是，点H对应数轴上的数是；
（2）如图（2），设∠AHF的平分线和∠AGH的平分线交于点M，若∠HAO=α，试用α来表示∠M的大小；
（3）如图（2），设∠AHF的平分线和∠AGH的平分线交于点M，设∠EFH的平分线和∠FOC的平分线交于点N，求∠N+∠M的值．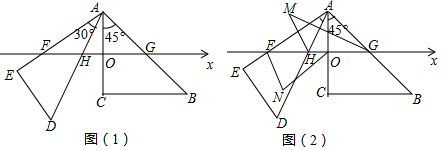
发布：2025/6/23 15:0:2组卷：481引用：11难度：0.1 -
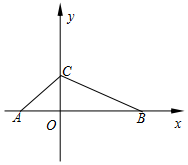2．如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（-2，0）、B（4，0）、C（0，2）．
（1）请用尺规作出△ABC的外接圆⊙P（保留作图痕迹，不写作法）；
（2）求出（1）中外接圆圆心P的坐标；
（3）若点C的坐标改为（0，a），其余条件不变，是否存在这样的点C使得∠ACB=45°？如果存在，请直接写出a的值；如果不存在，请说明理由．发布：2025/6/23 18:0:2组卷：113引用：2难度：0.1 -
3．如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC、BD的数量关系是；直线AC、BD的位置关系是．
（2）将图1的△OAB绕点O顺时针旋转90°角，在图2中画出旋转后的△OAB．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，连接AC、BD得到图3，这时（1）中的两个结论是否成立？作出判断并说明理由．若△OAB绕点O继续旋转更大的角时，结论仍然成立吗？作出判断，不必说明理由．
发布：2025/6/23 18:0:2组卷：92引用：1难度：0.5
