如图1，△ABC中，AB=AC，点D在AB上，且AD=CD=BC．
（1）求∠A的大小；
（2）如图2，DE⊥AC于E，DF⊥BC于F，连接EF交CD于点H．
①求证：CD垂直平分EF；
②直接写出三条线段AE，DB，BF之间的数量关系．
【考点】三角形综合题．
【答案】（1）36°；
（2）①证明见解析；②AE=DB+BF．
（2）①证明见解析；②AE=DB+BF．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 14:0:2组卷：823引用：5难度：0.3
相似题
-
1．已知：等边△ABC中．
（1）如图1，点M是BC的中点，点N在AB边上，满足∠AMN=60°，求的值；ANBN
（2）如图2，点M在AB边上（M为非中点，不与A、B重合），点N在CB的延长线上且∠MNB=∠MCB，求证：AM=BN．
（3）如图3，点P为AC边的中点，点E在AB的延长线上，点F在BC的延长线上，满足∠AEP=∠PFC，求的值．BF-BEBC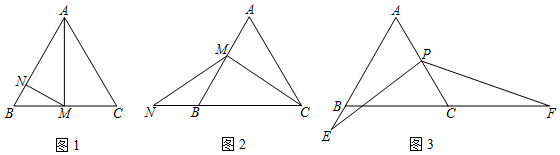
发布：2025/6/12 4:0:1组卷：1053引用：4难度：0.3 -
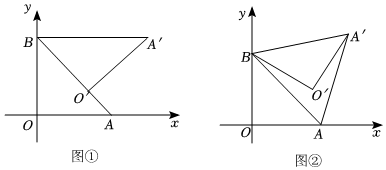2．在平面直角坐标系中，点A（2，0），点B（0，2）分别是坐标轴上的点，连接AB．把△ABO绕点B逆时针旋转得△A′BO′．点A，O旋转后的对应点为点A′，O′．记旋转角为α．
（Ⅰ）如图①，当点O′落在AB边上时，求α的值和点O′的坐标：
（Ⅱ）如图②，当α=60°时，求AA′的长和点O′的坐标：
（Ⅲ）连接AO′，直接写出在旋转过程中△AO′A′面积的最大值．发布：2025/6/12 4:30:1组卷：1018引用：7难度：0.1 -
3．我们发现，“用不同的方式表示同一图形的面积”可以解决计算线段的长度有关问题，这种方法称为面积法．
【问题探究】在△ABC中，D是BC边上的点（不与点B、C重合），连接AD．
（1）如图①，当点D是BC边上的中点时，S△ABD：S△ACD=；
（2）如图②，当AD是∠BAC的平分线时，若AB=m,AC=n,S△ABD：S△ACD（用含m,n的代数式表示）=；
【解决问题】如图③，在△ABC中，∠BAC=90°，AD平分∠BAC，AB=8，AC=6，求BD的长度．
发布：2025/6/12 3:0:1组卷：504引用：2难度：0.3
