如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正n边形（n＞4），观察每个正多边形中∠α的变化情况，解答下列问题：
（1）将下面的表格补充完整：
| 正多边形的边数 | 5 | 6 | 7 | … | n |
| ∠α的度数 |
36° 36°
|
60° 60°
|
540 ° 7 540 ° 7 |
… |
180°- 720 n 180°-
720 n |
（3）根据规律，是否存在一个正n边形，使其中的∠α=130°？若存在，直接写出n的值；若不存在，请说明理由．
【考点】多边形内角与外角；规律型：图形的变化类．
【答案】36°；60°；；180°-
540
°
7
720
n
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/19 8:0:9组卷：153引用：3难度：0.6
相似题
-
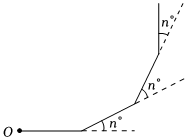1．如图，小明从点O出发，沿直线前进5米后向左转n°（0＜n＜90），再沿直线前进10米向左转相同的度数，……照这样走下去，小明发现：当他第一次回到了出发点时，共转过了24次，则小明每次转过的角度n的值为 ．发布：2025/6/8 10:0:2组卷：132引用：2难度：0.7 -
2．完成下面的证明：
如图．在四边形ABCD中，BE平分∠ABC交线段AD于点E，∠1=∠2，∠C=110°，求∠D的度数．
解：∵BE平分∠ABC（已知），
∴∠2=（ ），
又∵∠1=∠2（已知），
∴∠1=（ ），
∴AD∥BC（ ），
∴∠C+=180°（ ），
又∵∠C=110°（已知），
∴∠D=．发布：2025/6/8 11:30:1组卷：323引用：6难度：0.7 -
3．若一个正多边形的一个内角为144°，则这个图形为正（ ）边形．
发布：2025/6/8 8:0:6组卷：578引用：5难度：0.8
