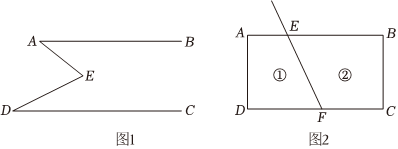
如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,求∠AED的度数?
②若∠A=20°,∠D=60°,求∠AED的度数?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系.
【考点】平行线的性质.
【答案】(1)①70°;②80°;③∠AED=∠EAB+∠EDC;
(2)当点P在①区域时,∠EPF=360°-(∠PEB+∠PFC);当点P在区域②时,∠EPF=∠PEB+∠PFC.
(2)当点P在①区域时,∠EPF=360°-(∠PEB+∠PFC);当点P在区域②时,∠EPF=∠PEB+∠PFC.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/4 8:0:5组卷:29引用:2难度:0.3