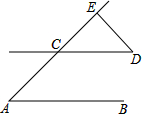
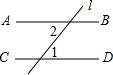将一副直角三角板如图1,摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度,顺时针方向旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.
(1)如图2,当AC为∠DCE的角平分线时,直接写出此时t的值;
(2)当AC旋转至∠DCE的内部时,求∠DCA与∠ECB的数量关系.
(3)在旋转过程中,当三角板ABC的其中一边与ED平行时,请直接写出此时t的值.

【答案】(1)此时t的值是3s;(2)∠ECB-∠DCA=15°;(3)t的值是15或33或24秒.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/30 8:0:9组卷:217引用:1难度:0.4