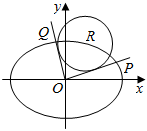
如图，在平面直角坐标系xOy中，已知R（x0，y0）是椭圆C：x224+y212=1上的一点，从原点O向圆R：（x-x0）2+（y-y0）2=8作两条切线，分别交椭圆于P，Q两点．
（1）若R点在第一象限，且直线OP、OQ互相垂直，求圆R的方程；
（2）若直线OP，OQ的斜率存在，并记为k1，k2，求k1k2的值．
x
2
24
+
y
2
12
【答案】（1）所求圆R的方程为；
（2）k1k2的值为。
（
x
-
2
2
）
2
+
（
y
-
2
2
）
2
=
8
（2）k1k2的值为
-
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：6引用：1难度：0.3
