观察以下等式:
第1个等式:13×(1+21)=2-11,
第2个等式:34×(1+22)=2-12,
第3个等式:55×(1+23)=2-13,
第4个等式:76×(1+24)=2-14.
第5个等式:97×(1+25)=2-15.
…
按照以上规律,解决下列问题:
(1)写出第6个等式:118×(1+26)=2-16118×(1+26)=2-16;
(2)写出你猜想的第n个等式:2n-1n+2×(1+2n)=2-1n2n-1n+2×(1+2n)=2-1n(用含n的等式表示),并证明.
1
3
2
1
1
1
3
4
2
2
1
2
5
5
2
3
1
3
7
6
2
4
1
4
9
7
2
5
1
5
11
8
2
6
1
6
11
8
2
6
1
6
2
n
-
1
n
+
2
2
n
1
n
2
n
-
1
n
+
2
2
n
1
n
【考点】规律型:数字的变化类;列代数式.
【答案】×(1+)=2-;×(1+)=2-
11
8
2
6
1
6
2
n
-
1
n
+
2
2
n
1
n
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/12 11:0:13组卷:2339引用:38难度:0.6
相似题
-
1.已知:a是不为1的有理数,我们把
称为a的差倒数.如:5的差倒数是11-a,-3的差倒数是11-5=-14,已知11-(-3)=14,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,以此类推,a2020的值为( )a1=32发布:2025/6/21 13:0:29组卷:104引用:3难度:0.6 -
2.一列数按某规律排列如下
,…若第n个数为11,12,21,13,22,31,14,23,32,41,则n=.56发布:2025/6/21 12:0:1组卷:1487引用:3难度:0.3 -
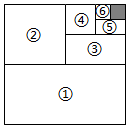 3.如图,将一个边长为1的正方形纸片分割成7个部分,部分1是边长为1的正方形纸片面积的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.阴影部分的面积是 ;受此启发,则+12+14+…+18的值为 .126发布:2025/6/21 12:0:1组卷:974引用:3难度:0.8
3.如图,将一个边长为1的正方形纸片分割成7个部分,部分1是边长为1的正方形纸片面积的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.阴影部分的面积是 ;受此启发,则+12+14+…+18的值为 .126发布:2025/6/21 12:0:1组卷:974引用:3难度:0.8


