如图1，在平面直角坐标系中，已知抛物线y=12x2+bx+c与x轴交于点A（-1，0），B（4，0），与y轴交于点C．
（1）求该抛物线的函数表达式及对称轴；
（2）如图1，若点M为对称轴上一动点，是否存在点M使△MAC的周长最小？若存在，求出点M的坐标；若不存在，请说明理由；
（3）如图2，点P是直线BC下方抛物线上的任意一点，连结PB，PC，以PB，PC为邻边作平行四边形CPBD，求四边形CPBD面积的最大值．
y
=
1
2
x
2
+
bx
+
c
【考点】二次函数综合题．
【答案】（1）抛物线的函数表达式为y=x2-x-2；对称轴为直线x=；
（2）存在点M使△MAC的周长最小，M坐标为（，-）；
（3）四边形CPBD面积的最大值是8．
1
2
3
2
3
2
（2）存在点M使△MAC的周长最小，M坐标为（
3
2
5
4
（3）四边形CPBD面积的最大值是8．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/26 21:0:8组卷：38引用：1难度：0.2
相似题
-
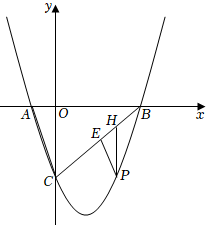1．如图，已知抛物线y=ax2+bx-3与x轴交于A（-1，0），B两点，与y轴交于点C且tan∠ABC=1，连接AC、BC．
（1）求抛物线的解析式；
（2）若P点是直线BC下方一点，过P点作PE∥AC交BC于点E，PH∥y轴交BC于点H，求CE+BH的最小值及此时P点的坐标．
（3）在第（2）条件下，将该抛物线向右平移2个单位后得到新抛物线，新抛物线与原抛物线相交于点F，点M为原抛物线对称轴上一点，在平面直角坐标系中是否存在点，使得以点H，M，N，F为顶点的四边形是菱形，若存在，请直接写出点N的坐标；如不存在，请说明理由．发布：2025/6/19 23:0:1组卷：226引用：2难度：0.3 -
2．如图1，二次函数y=ax2+bx的图象过点A（-1，3），顶点B的横坐标为1．
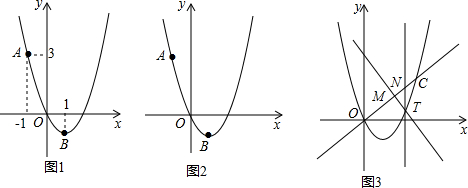
（1）求这个二次函数的表达式；
（2）点P在该二次函数的图象上，点Q在x轴上，若以A、B、P、Q为顶点的四边形是平行四边形，求点P的坐标；
（3）如图3，一次函数y=kx（k＞0）的图象与该二次函数的图象交于O、C两点，点T为该二次函数图象上位于直线OC下方的动点，过点T作直线TM⊥OC，垂足为点M，且M在线段OC上（不与O、C重合），过点T作直线TN∥y轴交OC于点N．若在点T运动的过程中，为常数，试确定k的值．ON2OM发布：2025/6/20 0:30:1组卷：1723引用：3难度：0.5 -
3．如图1，抛物线C1：y=x2-2ax-3a与x轴交于A、B两点，与y轴交于点C，且OC=3OA．
（1）求抛物线的解析式；
（2）抛物线上存在点P到直线BC的距离为h,且满足条件的点P恰有3个，求h的值；
（3）如图2，已知直线l：y=2x-3，将抛物线C1沿y=2x-3方向平移至C2，C2的顶点横坐标为m,与l相交于E、F两点，在x轴上存在一点P，使∠EPF=90°，求m的取值范围．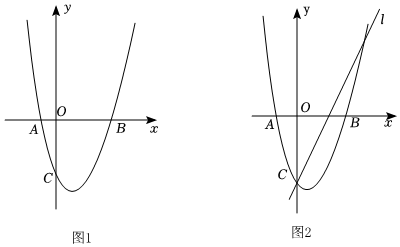
发布：2025/6/20 0:0:1组卷：71引用：2难度：0.2
