在▱ABCD中，∠ADC的平分线交BC于点E，交AB的延长线于点F，以BE，BF为邻边作▱BFGE．
（1）如图1，求证：▱BFGE是菱形；
（2）如图2，若∠BAD=90°，AB=2，BC=2，连接BG，交EF于点O，连接OA，OC，AC，求OA的长；
（3）如图3，若∠BAD=120°，连接AC，AG，求∠GAC的度数．
2
【考点】四边形综合题．
【答案】（1）见解析过程；
（2）AO=；
（3）60°．
（2）AO=
3
（3）60°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：83引用：4难度：0.3
相似题
-
1．阅读短文，解决问题
定义：三角形的一个角与菱形的一个角重合，且菱形的这个角的对角顶点在三角形的这个角的对边上，则称这个菱形为该三角形的“亲密菱形”．例如：如图1，四边形AEFD为菱形，∠BAC与∠DAE重合，点F在BC上，则称菱形AEFD为△ABC的“亲密菱形”．
如图2，在Rt△ABC中，∠B=90°，AF平分∠BAC，交BC于点F，过点F作FD∥AC，EF∥AB．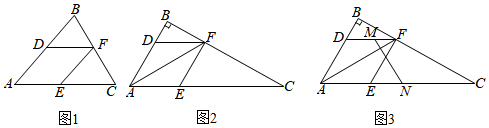
（1）求证：四边形AEFD为△ABC的“亲密菱形”；
（2）若AC=12，FC=2，求四边形AEFD的周长；6
（3）如图3，M、N分别是DF、AC的中点，连接MN．若MN=3，求AD2+CF2的值．发布：2025/6/20 0:30:1组卷：1098引用：9难度：0.6 -
2．（1）如图1，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF=45°．直接写出BE、DF、EF之间的数量关系；
（2）如图2，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是BC，CD上的点，且∠EAF=∠BAD，求证：EF=BE+DF；12
（3）如图3，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，延长BC到点E，延长CD到点F，使得∠EAF=∠BAD，则结论EF=BE+DF是否仍然成立？若成立，请证明；不成立，请写出它们的数量关系并证明．12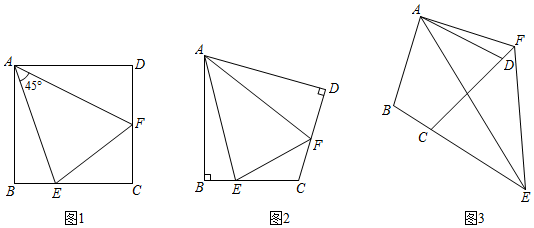
发布：2025/6/20 1:0:2组卷：1509引用：2难度：0.5 -
3．在正方形ABCD中，对角线AC，BD相交于点O，点E在线段OB上，点F在线段AD上，连接AE，连接EF交AC于点M，已知∠DEA=∠OME．
（1）如图1．求证：AE=EF：
（2）如图2，点N在线段F上，DN=EN，DN延长线交AC于H，连接CF，求证，CF=DH：2
（3）如图3，在（2）的条件下连接OF，当OF∥AE，AB=6时，直接写出线段OH的长．2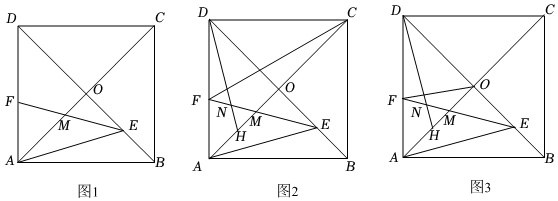
发布：2025/6/20 0:0:1组卷：112引用：1难度：0.4
