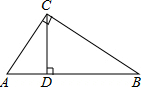
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．
（1）求证：AC2=AD•AB；
（2）求证：AC2+BC2=AB2（即证明勾股定理）；
（3）如果AC=4，BC=9，那么AD：DB的值是16：8116：81；
（4）如果AD=4，DB=9，那么AC：BC的值是2：32：3．
【考点】相似三角形的判定与性质；勾股定理的证明．
【答案】16：81；2：3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/11 8:0:2组卷：159引用：2难度：0.3
相似题
-
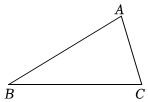1．如图，在△ABC中，∠C＞∠B．
（1）请用尺规作图法，在△ABC内求作∠ACD，使∠ACD=∠B，CD交AB于D．（不要求写作法，保留作图痕迹）
（2）在（1）的条件下，若AC=6，AB=9，求AD的长．发布：2025/5/24 0:30:1组卷：35引用：1难度：0.6 -
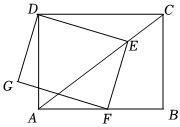2．如图，在矩形ABCD中，AB=8，AD=6，点E是对角线AC上一动点，连接DE，过E作EF⊥DE，交AB边于点F，以DE、EF为邻边作矩形DEFG．
（1）当CE=4时，则EF的长为．
（2）点H在DC上，且HD=1，连接HG，则HG长的最小值是 ．发布：2025/5/24 0:30:1组卷：1054引用：3难度：0.5 -
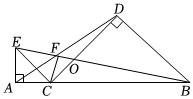3．如图，点C在线段AB上，在AB同侧作等腰Rt△ACE和等腰Rt△BCD，使∠EAC=∠BDC=90°，连接BE，分别交CD于点O，交AD于点F．
（1）求证：△ACD∽△ECB；
（2）若，AC=2，求AF的长．CB=42发布：2025/5/24 0:30:1组卷：233引用：1难度：0.5
