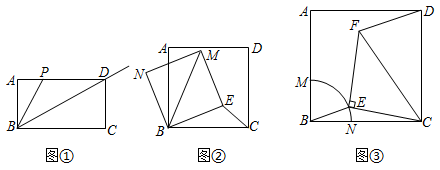
（1）问题提出：如图①，在矩形ABCD中，AB=1，BC=3，P是AD上一动点，则BP+12PD的最小值为33．
（2）问题探究：如图②，在正方形ABCD中，AB=3，点E是平面上一点，且CE=1，连接BE在BE上方作正方形BEMN，求BM的最大值．
（3）问题解决：为迎接2021年9月在西安举办的第14届全运会，打造体育历史文化名城，某小区对一正方形区域ABCD进行设计改造，方便大家锻炼运动．如图③，在正方形内设计等腰直角△CEF为健身运动区域，直角顶点E设计在草坪区域扇形MBN的弧MN上．设计铺设CF和DF这两条不同造价鹅卵石路，已知AB=40米，BM=102，∠CEF=90°，CE=EF，若铺设CF路段造价为每米200元，铺设DF路段的造价为每米100元，请求出铺设CF和DF两条路段的总费用的最小值．
3
1
2
3
3
2
【考点】圆的综合题．
【答案】
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/18 11:0:12组卷：164引用：1难度：0.3
相似题
-
1．在矩形ABCD中，AB=6cm,BC=12cm,点P从点A出发，沿AB边向点B以每秒1cm的速度移动，同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动，设两点移动的时间为t秒，回答下列问题：
（1）如图1，当t为几秒时，△PBQ的面积等于5cm2？
（2）如图2，当t=秒时，试判断△DPQ的形状，并说明理由；32
（3）如图3，以Q为圆心，PQ为半径作⊙Q．
①在运动过程中，是否存在这样的t值，使⊙Q正好与四边形DPQC的一边（或边所在的直线）相切？若存在，求出t值；若不存在，请说明理由；
②若⊙Q与四边形DPQC有三个公共点，请直接写出t的取值范围．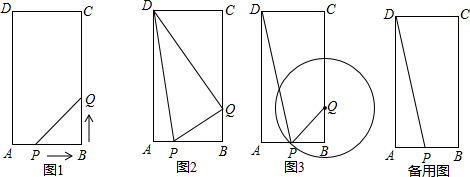
发布：2025/6/22 20:0:1组卷：554引用：8难度：0.3 -
2．如图，已知直线与两坐标轴分别交于A、B两点，⊙C的圆心坐标为（-2，0），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积S的取值范围是y=-3x+23．发布：2025/6/22 19:30:1组卷：340引用：3难度：0.7 -
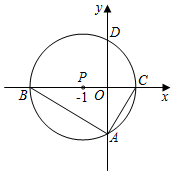3．如图，以点P（-1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．3
（1）求B、C两点的坐标；
（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；
（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．发布：2025/6/23 2:0:1组卷：676引用：30难度：0.1
