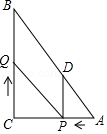
如图，在Rt△ABC中，∠C=90°，BC=8，AC=6，动点P从点A开始，沿边AC向点C以每秒1个单位长度的速度运动，动点D从点A开始，沿边AB向点B以每秒53个单位长度的速度运动，且恰好能始终保持连结两动点的直线PD⊥AC，动点Q从点C开始，沿边CB向点B以每秒2个单位长度的速度运动，连结PQ．点P，D，Q分别从点A，C同时出发，当其中一点到达端点时，另两个点也随之停止运动，设运动时间为t秒（t≥0）．
（1）当t=3时，求PD的长？
（2）当t为何值时，四边形BQPD的面积为△ABC面积的一半？
（3）是否存在t的值，使四边形PDBQ为平行四边形？若存在，求出t的值；若不存在，说明理由．
5
3
【考点】四边形综合题．
【答案】（1）PD的长为4；
（2）当t=9-3时，四边形BQPD的面积为三角形ABC面积的一半；
（3）t的值为．
（2）当t=9-3
5
（3）t的值为
12
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：188引用：3难度：0.3
相似题
-
1．如图，平面直角坐标系中O是原点，▱OABC的顶点A，C的坐标分别是（8，0），（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB于点F，G，连接FG．则下列结论：
①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是；④OD=203453
其中正确的结论是（填写所有正确结论的序号）．发布：2025/6/16 11:0:1组卷：3337引用：5难度：0.2 -
2．（1）[问题背景]如图1，在△ABC中，AB=AC，∠BAC=α°，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转α°得到AE，连接EC，则∠BCE=°（用含α的式子表示），线段BC，DC，EC之间满足的等量关系式为；
（2）[探究证明]如图2，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转90°得到线段AE，连接DE，求证：BD2+CD2=2AD2；
（3）[拓展延伸]如图3，在四边形ABCF中，∠ABC=∠ACB=∠AFC=45°，BF=3，CF=1．将△ABF绕点A逆时针旋转90°，试画出旋转后的图形，并求出AF的长度．（不要求尺规作图）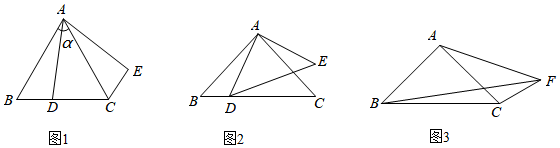
发布：2025/6/16 14:30:2组卷：1152引用：2难度：0.1 -
3．（1）如图①，把三角形纸片ABC沿DE折叠，当点A落在四边形BCED的内部时，若∠B=50°，∠C=85°，求∠1+∠2的值；
（2）如图②，如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部A′的位置，此时∠A与∠1、∠2之间存在什么样的等量关系？并说明理由；
（3）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D与∠1、∠2之间的等量关系吗？（直接写出关系式即可）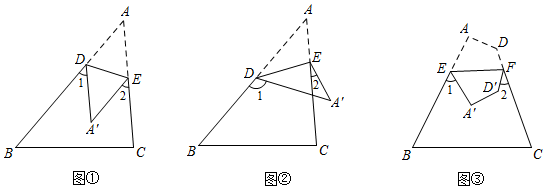
发布：2025/6/16 21:0:1组卷：229引用：2难度：0.4
